

A projectile, subject only to the force of gravity, travels a horizontal distance that is determined by its initial velocity and the angle from the horizontal at which it is launched.
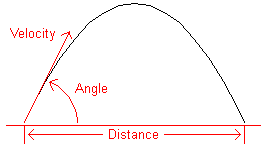
Write a program that implements a simple one-person game. The user begins by entering the distance the projectile is to travel. The user then has up to five opportunities to come up with a correct combination of initial velocity and angle to launch a projectile that travels the given distance (plus or minus 1.0%). The player wins as soon as (s)he enters a correct combination of velocity and angle. After five incorrect combinations, the player loses the game. In either case (win or lose), the player is asked if (s)he wants to play again.
For each combination of velocity and angle entered by the user, display the distance such a projectile would travel. If that distance is within 1.0% of the desired distance, display a message indicating that the player has won the game. After five unsuccessful tries, display a message indicating that the player has lost.
Before a game is started, the user is also asked whether (s)he wants to play the game. If so, (s)he should enter a 'y' or a 'Y'. Any other input will terminate the program. At the beginning of each game, the user enters the desired distance (in feet). At the beginning of each turn, the player enters the initial velocity (in feet/sec) and the angle (in degrees).
The formula for the horizontal distance is
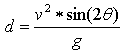
where d is the distance (in feet), v is the initial velocity (in ft/sec), θ is the angle (in radians), and g is the acceleration due to gravity (32.2 ft/sec/sec).
Your program should use a value-returning function that calculates and returns the horizontal distance.
Your program should use another value-returning function that returns a Boolean value indicating whether the calculated distance is within ±1.0% of the desired distance. If the value returned by this function is true then the player has won the game.
HORIZONTAL DISTANCE TRAVELED BY A PROJECTILE
In this game, you will enter the horizontal distance that a projectile
should travel. You will then be given up to five chances to enter the
correct combination of the initial velocity and the angle (above the
horizontal) at which the projectile should be launched. If you get the
correct combination within five tries then you win the game.
Do you want to play (Y or N)? y
Enter the horizontal distance (ft): 200
Enter initial velocity (ft/sec): 88
Enter angle (degrees): 45
Projectile Distance: 240.497
Enter initial velocity (ft/sec): 80
Enter angle (degrees): 45
Projectile Distance: 198.758
Congratulations! You won the game.
Do you want to play again (Y or N)? y
Enter the horizontal distance (ft): 200
Enter initial velocity (ft/sec): 88
Enter angle (degrees): 50
Projectile Distance: 236.843
Enter initial velocity (ft/sec): 88
Enter angle (degrees): 60
Projectile Distance: 208.276
Enter initial velocity (ft/sec): 88
Enter angle (degrees): 61
Projectile Distance: 203.953
Enter initial velocity (ft/sec): 88
Enter angle (degrees): 62
Projectile Distance: 199.381
Congratulations! You won the game.
Do you want to play again (Y or N)? y
Enter the horizontal distance (ft): 300
Enter initial velocity (ft/sec): 50
Enter angle (degrees): 45
Projectile Distance: 77.6398
Enter initial velocity (ft/sec): 100
Enter angle (degrees): 45
Projectile Distance: 310.559
Enter initial velocity (ft/sec): 110
Enter angle (degrees): 40
Projectile Distance: 370.068
Enter initial velocity (ft/sec): 90
Enter angle (degrees): 40
Projectile Distance: 247.731
Enter initial velocity (ft/sec): 105
Enter angle (degrees): 43
Projectile Distance: 341.557
I'm sorry, but you did not win the game.
Do you want to play again (Y or N)? n
Download the file Lab05.cpp and write the code for playing the game itself and complete the function definitions. I've written the rest of the code for you.
This project requires a nested loop which is a looping structure (the inner loop) within the body of another looping structure (the outer loop). The inner loop controls the play of the game itself and this is the part that you are to write. It has two termination conditions; the user has won or the user has made 5 unsuccessful guesses. The user wins if the calculated distance (based on the initial velocity and the angle) is within 1% of the specified distance. Notice that this loop is a combination of a counting loop (five unsuccessful guesses) and a sentinel-controlled loop (the calculated distance is within 1% of the specified distance).
The outer loop controls how many times the user plays the game. It is a sentinel-controlled loop since the user enters a 'y' or 'Y' to continue the game. We'll just assume that any other letter indicates that the user wants to quit. (Technically, we should require the user to enter 'n' or 'N' to terminate the program but that just adds another level of complexity.)
I have written the prototypes and the skeleton code for the two required functions. You have to write the code to implement them properly.