

Arithmetic expressions are commonly written using what is called infix notation in which each operator appears between its two operands. For example, in the expression 3 + 4, the first operand is 3 and the second is 4 and the addition operator is placed between them.
Consider the expression 8 - 10 * 3. Because multiplication has precedence over addition, it must be done first. The first operand for the multiplication operation is 10 and the second operand is 3.The first operand for the subtraction operation is 8 and the second operand is the result of 10 * 3 (or 30).
If we wanted the subtraction to be done first, we would have to use parentheses: ( 8 - 10 ) * 3. The operands for the subtraction operation are 8 and 10. The operands for the multiplication operation are -2 (the result of the subtraction operation) and 3.
Because of operator precedence and parenthetical expressions, the logic to read an infix expression and generate the correct mathematical result is rather complicated. This complexity is introduced, primarily, by the fact the operations are not performed in the same order in which they appear in the expression (i.e., left to right). Instead the order is determined by operator precedence and placement of parentheses.
In postfix notation (also called reverse polish notation), each operator appears after its two operands. For example, the infix expression 3 + 4 would be written in postfix notation as 3 4 +.
The infix expression 8 - 10 * 3 would be written in postfix notation as 8 10 3 * -. The operands for the multiply operation are 10 and 3 yielding a result of 30. The operands of the subtraction operation are 8 and 30 (the result of the multiplication operation) yielding a final result of -22.
The infix expression ( 8 - 10 ) * 3 would be written in postfix notation as 8 10 - 3 *. The operands of the subtraction operation are 8 and 10 yielding a result of -2. The operands of the multiplication operation are -2 (the result of the subtraction operation) and 3 yielding a final result of -6
In a postfix expression, the operations are always performed in the order in which the appear (left to right) and there is never any need for parentheses. Consequently, it is relatively easy to read in a postfix expression and generate the correct mathematical result.
In this assignment, you will complete a program that converts an infix expression (stored as an ordinary string) to the corresponding postfix expression and then evaluates the postfix expression. Some of the work has been done for you in the file Hmwk07.cpp. This file contains a main driver and stubs. It will compile and execute but, since the functions are not fully implemented, it does not yet work. Add your name as coauthor and complete the function implementations.
The individual components that make up the infix expression are referred to as tokens. There are two possible kinds of tokens: operands and operators. Operands are numbers. Operators are nonnumeric characters and include "+", "-", "*", "/", "(", and ")". To keep things as simple as possible, we will specify that our infix expressions are space-delimited. There is at least one space between any two successive tokens. This is not normally required as illustrated in this expression which has no spaces but makes perfect sense:
23+13*(8-11)/2
In our program, this expression will be written as
23 + 13 * ( 8 - 11 ) / 2
We will implement a token as a structure containing both a double value (if the token is an operand) and a string value (if the token is an operator). Such a structure could be used for either type of token. If the token is an operator then the operator will be stored in the string field. If the token is an operand, the number will be stored in the double field.
The problem is that given a specific token, how do you know whether to access the operand field or the operator field? You know it is one or the other but how can you tell which it is? One easy solution is to add a boolean field to the structure. Suppose we add a bool type variable named "isOperand". If isOperand is true then the token is an operand and we would know to access the double value stored in the operand field. However, if isOperand is false then the token is an operator and we would know to access the character stored in the operator field.
The convertToPostfix function returns the postfix expression (a list of tokens) as an out parameter. Traversing this postfix expression allows us to display the postfix expression on the standard output device and to evaluate it.
Here is a pseudo-code version of an algorithm to convert an infix expression into a postfix expression:
Push (Null)
While getToken
Case token Of
Operand: Append(token)
"(": Push(token)
")": While TOS <> "(" Do
Append(TOS)
Pop
Endwhile
Pop
Operator: While Precedence(token) <= Precedence(TOS) Do
Append(TOS)
Pop
Endwhile
Push(token)
Endcase
EndWhile
While TOS <> Null Do
Append(TOS)
Pop
Endwhile
Pop
As you can see, this algorithm requires the use of a stack of tokens. In effect, this stack keeps track of pending operations that have been deferred because of subsequent operations with a higher precedence.
The precedence function returns the precedence of an operation based on the table below. Note that, as you would expect, multiplication and division have a higher precedence than addition and subtraction.
Operator Precedence ( , "" 0 + , - 1 * , / 2
The valueOf function returns the value of its postfix parameter as a double value. A postifix expression is evaluated by traversing the list of tokens sequentially from beginning to end. Every time an operand is encountered, its value is pushed onto a stack of doubles. Whenever an operator is encountered, the operation is applied to the top two elements of the stack (which are removed from the stack) and the result is pushed onto the stack. In effect, the two operands are replaced by the result of the arithmetic operation. When you reach the end of the postfix expression, the stack should contain only one value which is the value of the postfix expression. If there is not exactly one value left on the stack, than an error has occurred and your should generate an appropriate error message.
A stringstream object allows you to convert an ordinary string into a stream (like cin or an ifstream object). Once the stringstream object has been initialized, you can extract input from the stringstream object using the normal (white-space delimited) extraction operator just as you can for any other input stream.
In Hmwk07.cpp (in main), you'll see that we get the infix expression from the standard input as a line of text using getline. However, we want to parse this line of text in order to extract the tokens (space-delimited operands and operators) that make up the infix expression. We could do this on a character by character basis using functions in the string class. However, a much easier approach is to convert this string to a stringstream object and extract the tokens using the extraction operator (which is designed to extract whitespace-delimited tokens).
At the very beginning of the body of the loop, we initialize the stringstream object using the str function:
infixStream.str(infixExpr);
The stringstream object is then passed to the routine that generates the postfix expression:
convertToPostfix(infixStream, postfixExpr);
Within the convertToPostfix function, the corresponding formal parameter, "infix", can be used just like cin or an ifstream variable. You extract and process tokens (as strings) using the extraction operator until the stream fails:
infix >> tokenString;
while (!infix.fail())
{
// process the token
infix >> tokenString;
}
Notice that immediately after the invocation of convertToPostfix back in main, we clear the stringstream object so we can reuse it again the next time through the loop. (Recall, that once a stream fails, it remains in the failed state and can not be used again until it is cleared.)
You are to use a linked list to store your postfix expression. However, there is one slight problem with the algorithm given above for generating a postfix expression. You may have noticed that it requires an append operation that adds a new token to the end of the postfix expression. What you need to do is add a push_back function to your list class. This function inserts an item at the end of the list. I've provided the code for this function in push_back.htm. (Your program would be more efficient if you rewrote your list class to use a tail pointer and then implemented a push_back function. However, I don't want you to spend that much time on this project.)
Copy your list class implementation to a new file named "list.cpp" and add the code for the push_back function. Make sure the list.cpp file is in the same folder as your Hmwk07.cpp file.
The image below shows a sample run of this application. Don't forget that the infix expression must be space-delimited. You MUST include at least one space between each token and the next. Otherwise, bad things will happen.
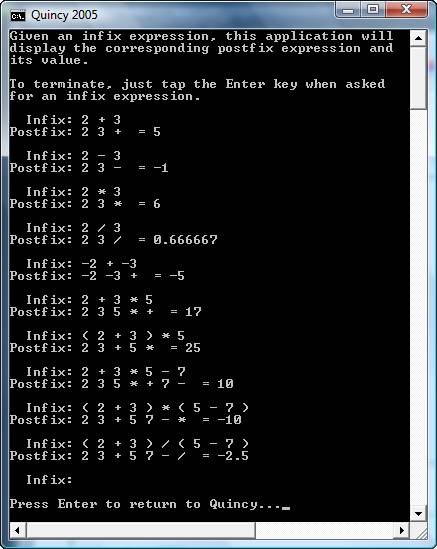
This assignment is an example of a good, non-trivial use of stacks. Since you have been given the infix to postfix algorithm, you should find it relatively easy to implement the postfix function. I will remind you that in homework 1, we used the strtod function to help us convert a string to a decimal value. You will find that function useful in this context as well since you need to convert each operand from a string representation to the corresponding numeric representation.
Submit your completed Hmwk07.cpp file as an email attachment.