

In this assignment, you will write a program that simulates a waiting line. There are three basic components to the simulation; clients, the waiting line, and servers. Clients represent entities that require some sort of action. The time required to perform the action may vary from client to client and clients arrive at random times.
As clients arrive, they move to the end of the waiting line (no cuts allowed). In some cases, there may be more than one waiting line in which case clients move to the end of the shortest waiting line. However, in our simulation, we will have only one waiting line.
Servers perform the action required by the clients. When they are done servicing a client, the first client in the waiting line will be the next client served. A single waiting line may be served by more than one server. If there are multiple waiting lines, each line is usually served by a single server. In our case, we will have a single server serving our single waiting line.
A time-driven simulation simulates such a system by determining the state of the system at discrete moments of time. The time interval depends on the type of system being simulated. For example, if you are simulating processes waiting for service by a CPU, the time interval might be a millisecond or even a microsecond. If you are simulating a waiting line in a busy post office, the time interval might be a minute. If you are simulating complex jobs like bricking the exterior of a house, the time interval might be a hour.
In any case, the simulation generally consists of a for loop that, like a clock, counts time intervals beginning at 0 up to the desired duration of the simulation. For each tick of the "clock", the simulation determines whether a new client arrives and if so sends it to a waiting line. It then removes clients from servers that have just finished serving the client. Finally, if any servers are free (including those that have just become free) the program moves a client from a waiting line to the server (if there are any clients in line, of course).
When the stop time is reached there may still be clients waiting in line. We could just ignore them or, more realistically, we continue running the clock until all clients have been served. However, no new clients are added to the line after the stop time.
Your program will employ a single waiting line and a single server. At the end of the time specified by the user, the server will continue to serve the clients that were already in line but no new clients will be added to the line. Your program should display the specified duration of the simulation, the actual duration, the arrival probability, the range of service times, the number of clients served, the average wait time and the maximum wait time.
The user will enter, interactively, the following:
The sample run shown below indicates how the input and output will be formatted on the computer screen.
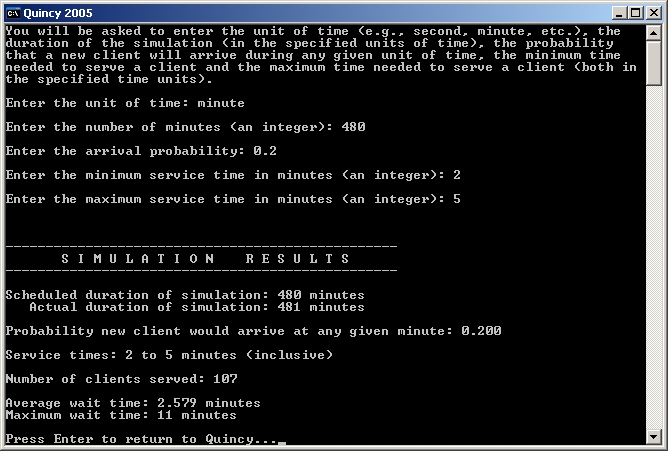
The simulation will be coded within a counting loop that counts from 0 to the length of time the simulation is to run. Each time through the loop, you will perform the following tasks:
At some point you will need to update the variables that allow you to calculate the average wait time and the maximum wait time. You can do this when the client leaves the waiting line or, if you prefer, do it when the client leaves the server.
Use a uniform probability distribution to determine the length of time required to serve a client. For example, suppose the shortest service time entered by the user is 2 and the longest is 5. In that case, there are four possible service times (2, 3, 4, or 5 units of time) each with a probability of 1/4.
The waiting line itself is modeled by a queue object. A client is added to the rear of the queue and served when it reaches the front of the queue and the server is free.
I've done some of the work for you in Hmwk09.cpp. Add your name as co-author and send your final version to me as an email attachment.