

The first two numbers in the Fibonacci sequence are both 1. Each Fibonacci number after the second is the sum of the previous two values. For example, the third value is 2 (the sum of the first two values). The fourth Fibonacci number is 3 (the sum of the second and third numbers). Here is a recursive definition of the nth Fibonacci number:
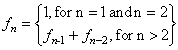
Display the first n Fibonacci numbers using the output format shown below.

Ask the user to enter the number of terms to display.
Calculate the first n Fibonacci numbers.
Implement a recursive function named "fib1" that has one integer parameter, n, and returns the nth Fibonacci number as an integer. This function should implement the recursive definition given above.
Implement a non-recursive function named "fib2" that has one integer parameter, n, and returns the nth Fibonacci number as an integer. This function should use a looping structure to calculate the nth Fibonacci number.
Your main program should include a loop that counts from 1 to n (the value entered by the user). Each time through the loop you should invoke only one of these two functions to calculate the nth Fibonacci number. For example, if you invoke fib1 then fib2 will not be used during the execution of your program. Your program output should be exactly the same no matter which function you invoke.
Experiment with your program and when you submit your program, tell me, in your email message, which fibonacci function is faster and how you arrived at your conclusion experimentally. Finally, try to explain what it is about the slower implementation that causes it to be slower.
Name your program file "Lab02.cpp" and submit it to me as an email attachment.