

On the digital logic page, we looked at designing a circuit to implement a function that was defined by a truth table. In particular, the function was given by the sum of products expression for the truth table. While, the sum of products expression is guaranteed to be correct, it is seldom optimal. That is, it is often possible to find a simpler, equivalent expression that requires fewer gates and/or gates with fewer inputs; both of which make the circuit cheaper to build. Simplifying the sum of products expression involves algebraic manipulation of the expression using the laws of Boolean algebra. A Karnaugh map is a graphical approach to algebraic simplification.
Basically, a Karnaugh map is a rectangular grid of cells where each cell corresponds to the product expression for a row in the truth table. Consequently, there are as many cells in a Karnaugh map as there are rows in the corresponding truth table. Recall that the number of rows in a truth table with n variables is given by 2n. The arrangement of the cells in a Karnaugh map is critical. Here is the template for a two-variable table (with variables named A and B):
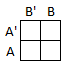
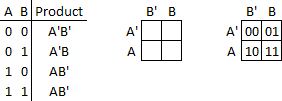
The row and column headings indicate the product represented by the cell. For example, the upper-left cell corresponds to the product A'B' and the lower-right cell corresponds to the product AB. You can also think of each cell representing the combination of truth values for the variables in the corresponding row. For example, the product A'B' corresponds to the truth values 00 and the product AB corresponds to the truth values 11:
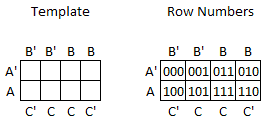
The template for a 3-variable map is given below. The figure to the left is the template and the figure to the right shows the corresponding row numbers (in binary).
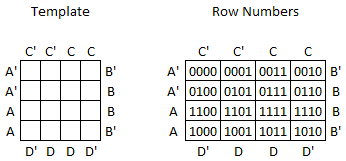
The template for a 4-variable map is given below. The figure to the left is the template and the figure to the right shows the corresponding row numbers (in binary).
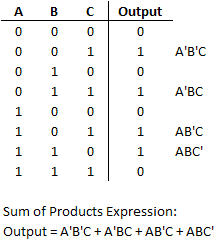
Consider the function whose truth table and sum of products expression is shown below.

Step 1: Create an empty map using the 2-variable template.

Step 2: Enter a 1 into each cell represented in the sum of products expression (cells A'B and AB).
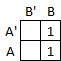
Step 3: Circle rectangular blocks of contiguous cells that contain 2 or 4 ones. The goals are to include as many ones as possible in each block and to include as many ones as possible in some block. In this case there is only one such block; the 2 cells in the second column.
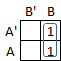
Step 4: Write a new expression that includes one term for each group of cells (including single cells that are not part of a larger group). For a single cell, the term is the normal product. For a group of cells, the term is a product formed from the factors in common to every cell in the group. In this simple example, there is only one group so there is only one term. The only factor in common to both cells in that group is B so the term associated with that group is B.
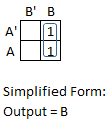
There are three things that make this process work. The first is that finding the factors common to all of the cells in a block is equivalent to finding a common factor in the corresponding terms in the sum of products expression. The second thing that makes this process work is that when you factor out the common factor in those terms, the other factor is always equal to 1 so what you are left with is just the common factor. In this example, the block contains both terms in the sum of products expression and these two terms have a common factor of B:
Output = A'B + AB = B(A' + A) = B(1) = B
We'll take a look at the third thing that makes this work in the examples below.
Consider the function whose truth table and sum of products expression is shown below.
Step 1: Create an empty map using the 3-variable template.
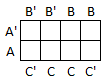
Step 2: Enter a 1 into each cell represented in the sum of products expression.
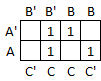
Step 3: Circle rectangular blocks of contiguous cells that contain 2, 4, or 8 ones. The goals are to include as many ones as possible in each block and to include as many ones as possible in some block. In this case there are 2 blocks containing 2 cells each.
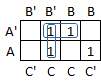
Step 4: Write a new expression that includes one term for each group of cells (including single cells that are not part of a larger group). For a group of cells, the term is a product formed from the factors in common to every cell in the group.
The simplified form of this function is the sum of these products.
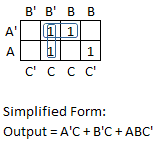
The horizontal block corresponds to the following:
A'B'C + A'BC = A'C(B' + B) = A'C(1) = A'C
The vertical block corresponds to the following:
A'B'C + AB'C = B'C(A' + A) = B'C(1) = B'C
There is, however, a problem because you can't perform both of these factorizations in the original sum of products expression:
Output = A'B'C + A'BC + AB'C + ABC' = A'C(B' + B) + AB'C + ABC' = A'C + AB'C + ABC' or Output = A'B'C + A'BC + AB'C + ABC' = B'C(A' + A) + A'BC + ABC' = B'C + A'BC + ABC'
The third property that was mentioned above comes into play in this example. In digital logic:
A = A + A
If A is 0 then A + A is also 0 and if A is 1 then A + A is also 1. Consequently, I can take any term in a sum of products expression and add it to the expression without changing the value of the expression. In this example, the term A'B'C appears in both blocks (and thus in both factorizations) but it only appears once in the original sum of products expression. But I can add that term to the expression without changing its value:
Output = A'B'C + A'BC + AB'C + ABC'
= A'B'C + A'BC + A'B'C + AB'C + ABC'
= A'B'C + A'BC + A'B'C + AB'C + ABC'
= A'C(B' + B) + B'C(A' + A) + ABC'
= A'C + B'C + ABC'
Consider the function whose truth table and sum of products expression is shown below.
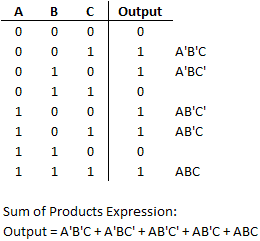
Step 1: Create an empty map using the 3-variable template.

Step 2: Enter a 1 into each cell represented in the sum of products expression.
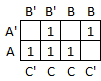
Step 3: Circle rectangular blocks of contiguous cells that contain 2, 4, or 8 ones. The goals are to include as many ones as possible in each block and to include as many ones as possible in some block. In this case there are 3 blocks containing 2 cells each.
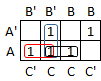
Step 4: Write a new sum of products expression that includes one term for each group of cells (including single cells that are not part of a larger group). For a group of cells, the term is a product formed from the factors in common to every cell in the group.
The simplified expression is the sum of these products.
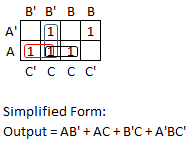
Notice that the term AB'C is common to all three groups. Consequently, I will need two more of these terms in the sum of products expression. Here is the equivalent algebra:
Output = A'B'C + A'BC' + AB'C' + AB'C + ABC
= A'B'C + AB'C + A'BC' + AB'C' + AB'C + ABC + AB'C
= A'B'C + AB'C + A'BC' + AB'C' + AB'C + ABC + AB'C
= B'C(A' + A) + A'BC' + AB'(C' + C) + AC(B + B')
= B'C + A'BC' + AB' + AC
In a 3-variable Karnaugh map, the left edge of the map and the right-edge are connected. You can think of the map as a tube that has been cut along its length and unrolled. This means that a block of cells can include cells in just the first and last columns. In the example below, the block "circled" in red has factors A' and C' in common so the corresponding term is A'C'.
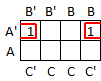
In the next example, the block "circled" in red contains only the factor C' in common so the term is just C'.
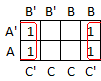
Here is the equivalent algebra for the example above:
Output = A'B'C' + A'BC' + AB'C' + ABC'
= C'(A'B' + A'B + AB' + AB)
= C'(A'(B' + B) + A(B' + B))
= C'(A' + A )
= C'
In a 4-variable Karnaugh map, the left and right edges are connected and the top and bottom edges are connected. (I have been unable to visualize that as any three dimensional object.) In the example below, the group of 2 has factors A', B', and D' in common so the corresponding term is A'B'D'.
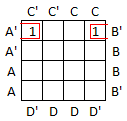
In the next example, the block of 4 has the factors B' and D in common so the term is B'D.
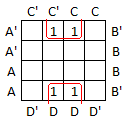
This next example is probably the strangest of all because it wraps around both vertically and horizontally. The group of 4 has only the factors B' and D' in common so the term is B'D'.
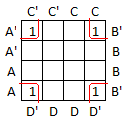
Finally, in the example below, the group of 8 has only the factor D' in common so the corresponding term is just D'.
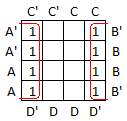
Consider the function whose truth table and sum of products expression is shown below.

Step 1: Create an empty map using the 4-variable template.
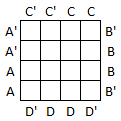
Step 2: Enter a 1 into each cell represented in the sum of products expression.
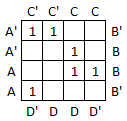
Step 3: Circle rectangular blocks of contiguous cells that contain 2, 4, 8 or 16 ones. The goals are to include as many ones as possible in each block and to include as many ones as possible in some block. In this case there are 4 blocks containing 2 cells each.
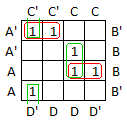
Step 4: Write a new sum of products expression that includes one term for each group of cells (including single cells that are not part of a larger group). For a group of cells, the term is a product formed from the factors in common to every cell in the group.
The simplified expression is the sum of these products: Output = A'B'C' + ABC + B'C'D' + BCD.
A'B'C'D' is included in 2 blocks as is ABCD. Consequently, the first thing I need to do is add each term a second time to the expression. Then I can group the terms into 4 groups of 2, factor out the common term from each group, and simplify:
Outcome = A'B'C'D' + A'B'C'D + A'BCD + AB'C'D' + ABCD' + ABCD
= A'B'C'D' + A'B'C'D + A'BCD + ABCD + AB'C'D' + A'B'C'D' + ABCD' + ABCD
= A'B'C'D' + A'B'C'D + A'BCD + ABCD + AB'C'D' + A'B'C'D' + ABCD' + ABCD
= A'B'C'(D + D') + BCD(A' + A) + B'C'D'(A + A') + ABC(D' + D)
= A'B'C' + BCD + B'C'D' + ABC