

In compound interest problems, a single investment is made and interest is paid to the lender periodically by adding the interest to the balance. The total interest paid is greater than it would be in a simple interest problem.
If $1,000 is invested for 1 year at 4% compounded monthly, how much will be in the account at the end of the year? The phrase "compounded monthly" means that the interest is calculated each month and added to the account. In general, the word following "compounded" indicates the length of the period. The table below lists the common periods and the corresponding number of periods per year (ppy).
| Compounded | Period | ppy |
| annually | one year | 1 |
| semiannually | six months | 2 |
| quarterly | three months | 4 |
| monthly | one month | 12 |
| daily | one day | 365 |
The periodic interest rate is calculated by dividing the nominal annual rate by the number of periods per year. The number of periods in the term is the time in years multiplied by the number of periods per year.
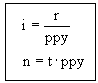
The table below illustrates the growth of our example investment. There is one row for each period of the term. The first row (Period zero) is included to make the graph of the final balances look better. For all practical purposes, the end of period zero and the beginning of period one are at the same time. All table entries are rounded off to the nearest cent.

The initial balance is the amount in the account at the beginning of the period. The present value is the final balance for period zero. For all remaining periods, the initial balance is the final balance from the preceding period.
The periodic interest is the amount of interest earned during the period. The periodic interest is calculated by multiplying the periodic rate times the initial balance.
![]()
The final balance is the amount in the account at the end of the period. The final balance is the sum of the initial balance and the periodic interest.
![]()
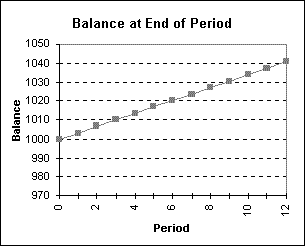
The future value is the final balance at the end of the last period. For this investment, the future value is $1040.74. Notice that the total interest earned is $40.74 compared to the $40 that would have been earned at 4% simple interest.
A graph of the final balances shows the growth of the investment during the year. By including the fictitious period zero in the table, the graph can include the present value as the first data point.
Creating a table like the one above for a generic problem leads to the compound interest formulas summarized below. Click here for the algebraic details. These formulas do not take rounding into account so calculated values may not give the correct results. For normal investments the error is limited to a few cents.
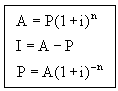
Savings bonds are investments that earn compound interest. Savings bonds are often given as gifts and sometimes as awards. The face value of the bond is the amount printed on the face of the bond and is the future value of the bond. For example, a $100 savings bond is worth $100 at the end of it's term. You can't cash it in for $100 until the bond has matured (reached the end of its term). The cost of buying a savings bond is the present value of the bond and is always less than the face value.
It is difficult to compare interest rates that have different compounding frequencies. For example, is 6% compounded monthly a better rate than 6.01% compounded quarterly? For any given interest rate and compounding frequency, the annual percentage yield (APY) is the equivalent interest rate compounded annually. The annual percentage yield is also called the annual effective rate or just the effective rate. In effect, the APY is the interest earned on an investment of one dollar for one year. The APY is usually expressed as a percent. Click here for algebraic details.
![]()