

A Christmas club account is a regular savings plan whose future value is intended to be used for expenses at Christmas time. Suppose that $100 is deposited into such an account at the end of the month for a year (December 31 through November 30 of the following year). Assume that the account pays 4.2% compounded monthly. How much is in the account immediately after the last deposit?
A table showing the growth of the account can be created similar to the tables illustrating the compound interest problems in the previous section. One new column, showing the amount deposited at the end of each month, is needed.
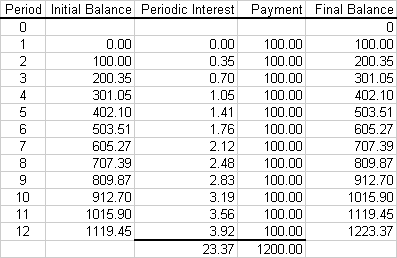
The fictitious period zero is included to make the graph (below) look nicer. The final balance at the end of period zero is zero since the first deposit is made at the end of the first period so there is nothing in the account at the beginning of the first period. As before, the initial balance for all periods following period zero is the final balance from the preceding period. The periodic interest is the initial balance times the periodic interest just as it was in the compound interest tables. The final balance for any period is the sum of the initial balance, the periodic interest, and the payment made at the end of the period.
Notice that the future value ($1,223,37) can be found by adding the total interest ($23.37) to the total of the deposits ($1,200.00).
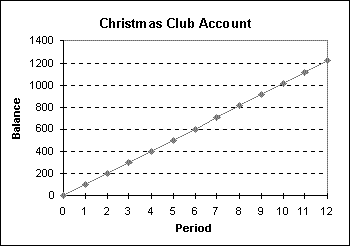
The graph below shows the growth of the balance in the Christmas Club account.
The annuity formulas used to solve savings plan problems are summarized below. Click here for the algebraic details. These formulas do not take rounding into account so calculated values may not give the correct results. For normal investments the error is limited to a few cents.
