

With a loan, part of each periodic payment pays the current period's interest and the rest is used to reduce the balance owed. The amount borrowed is the present value of the loan. The annuity formulas used to solve loan problems are summarized below. They can be derived from the savings plan formulas we used earlier. Click here for the algebraic details. As usual, these formulas do not take rounding into account and are not always exactly correct.
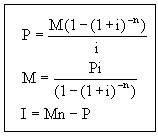
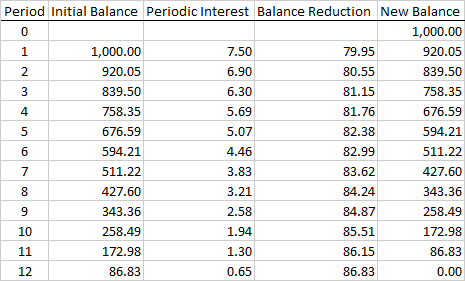
A table showing the decline in the balance (the amount owed) is called an amortization table. It is similar to the tables you have already seen but requires one more column: balance reduction. The balance reduction column shows how much of each payment is used to pay back the loan (and thereby reduce the balance).
Consider a 12-month loan of $1,000 at 9% compounded monthly. The monthly payment is $87.45. The amortization table for this loan is shown in the illustration below. Notice that the last entry in the Balance Reduction column has been set equal to the Initial Balance for that row rather than the payment minus the interest. This actually results in a slightly higher payment (87.48 rather than 87.45). A slight adjustment in the final payment is usually necessary since the periodic payment has been rounded off to the nearest penny.
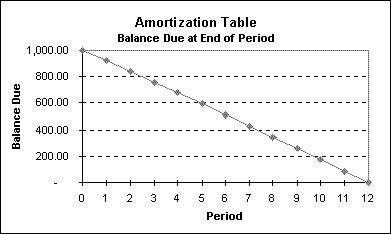
As before, the row corresponding to period 0 is included to make the graph of the final balances look better. The amount borrowed will appear on the y-axis (see below).
The initial balance in period 1 is the amount borrowed (the present value of the annuity). The periodic interest, as always, is the initial balance times the periodic interest rate. The balance reduction is simply the payment minus the periodic interest. Lastly, the final balance is the initial balance minus the balance reduction amount.
The decline in the balance due is illustrated in the graph below.
When we first looked at one-time investments, we defined the annual percentage yield (APY) as the amount of interest on one dollar for one year expressed as a percent. The primary purpose of the APY was to allow us to easily compare two investments with different compounding frequencies. By finding the APY of each we can determine which is giving us the best return (the one with the higher APY).
In the context of a loan, the term annual percentage yield is confusing to the customer because the customer is paying interest not receiving interest. Whatever yield there is in this investment goes to the lending institution not the customer. In this context, what we have been calling the annual percentage yield is referred to as the annual percentage rate (APR) or annual equivalent rate (AER). As before, its primary purpose is to allow consumers to more easily compare loan offers. Since APR is just another name for APY, it is calculated in exactly the same way:
![]()