

1. Download and open the workbook LoansLab01.xlsx. Remind me how. Enter your name in cell B1.
A couple borrows $12,000 to buy a new car. Their interest rate is 6.99% compounded monthly. The term of the loan is five years.
2. Enter the nominal interest rate, the periods per year, the number of years, and the present value as numbers. Enter the periodic rate, the number of periods, the periodic payment (see formula below), the total interest, and the annual percentage rate as Excel expressions using cell references. The payment should be rounded to the nearest penny (using Excel's ROUND function) since it will be used later on to calculate the balance reduction in the amortization schedule. You should get a value of $237.56. The annual percentage rate should be displayed as percent to 3 decimal places.
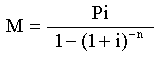
3. As you have done before, fill the "End of Period" column with a sequential series from 0 to the number of periods.
4. The new balance due at the end of period zero is the amount that was borrowed. In cell E16, enter a formula with the corresponding cell reference.
5. Starting with period one, the initial balance due is the new balance from the end of the previous period.
6. The periodic interest is always the initial balance times the periodic rate rounded to the nearest penny.
7. In savings problems the periodic interest was paid to you. In a loan problem, however, you pay the interest to the bank. The rest of the payment is used to reduce the balance you owe to the bank. For each period, the balance reduction is the difference between the payment (up in cell B3) and the periodic interest. Enter the formula for the balance reduction in cell D17.
8. The new balance is the initial balance minus the balance reduction. Enter the corresponding expression in cell E17.
9. Highlight cells B16:E17 and set the format to the comma format.
10. Copy the formulas in B17:E17 down one row. Make sure all of the values in row 18 are correct. If they are not, then correct the formulas in row 17 and repeat this step until the values in row 18 are correct.
11. Copy the formulas down the rest of the table. You should get negative twenty one cents as the new balance due at the end of the last period. (If you did not, then you probably forgot to round off the periodic interest to the nearest cent or you forgot to round off the payment to the nearest cent.) Why isn't the balance due at the end of the last period zero?
12. In the last period, the balance reduction formula must be modified (since the payment is a little too big). Since you will be paying off your loan, the balance reduction is equal to the initial balance for that period. Modify the formula for the balance reduction in cell D76 accordingly. Adjusting the balance reduction in the last row will result in a final balance of exactly zero.
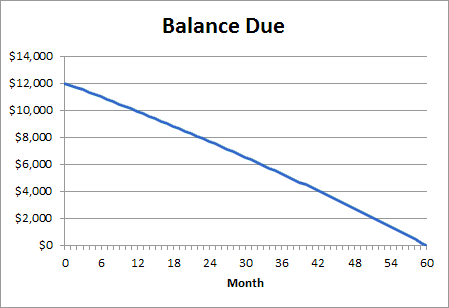
13. Insert a line chart to illustrate how the balance due decreases over time. Format the chart as shown here:
14. Following the instructions below, insert an "Area" chart to illustrate how the allocation of the payments (periodic interest and balance reduction) changes over time.
a. For this graph we are charting two sets of values which we will want to identify with labels. To include the column headings as labels, highlight the "Interest" and "Balance Reduction" column headings when you highlight these two columns of data.
b. Insert an Area chart. The subtype is "Stacked Area" (the second one in the first row).
c. Set the horizontal axis labels to the values in the period column, as usual.
d. Set the chart title to "Payment Allocation". The horizontal axis title is "Month". No vertical axis title is needed.
e. Format the vertical axis as currency to 0 decimal places.
f. Using the "Legend" tool, turn off the legend.
g. Use the "More Data Label Options" option on the "Data Labels" tool to add a data label to each section of the area chart. Uncheck the "Values" box and check the "Series Name" box. You'll need to do this twice; once for the blue area (Interest) and again for the reddish area (Balance Reduction). Your final chart should look something like this:
Notice that the amount of each payment allocated for interest declines slowly over time and the amount allocated for balance reduction increases slowly.
1. Suppose a young couple wanted to buy a house. To do so they would need a mortgage. A mortgage is just a loan with the house as the collateral. They take on a 30-year mortgage of $75,000 at 8.05% compounded monthly.
2. Write down your guess for the monthly payment on this mortgage and the total interest that the couple will pay:
M=
I=
3. Activate the "Mortgage" sheet and enter your name in cell B1. Enter the nominal annual rate, the periods per year, the number of years, and the present value. Enter the formulas for periodic rate, number of periods, periodic payment, total interest, and annual percentage rate. Don't forget to round the periodic payment to the nearest penny and format the annual percentage rate as a decimal to three decimal places.
4. Were your guesses very close?
5. Complete the amortization schedule for this mortgage. If necessary, don't forget to adjust the balance reduction amount for the last line of the table.
6. Insert a line chart illustrating how the balance due decreases over time.
7. Insert a stacked area chart showing how each payment is split between interest and balance reduction.
Use the same basic layout that was used in the examples above. For each problem, generate a period by period table, a line chart illustrating how the balance changes over time, and a stacked area chart showing how each payment is divided between interest and balance reduction.
A man borrows $2,000 to buy a new surround sound TV package. He takes out a loan at 18% compounded monthly for three years. What are his monthly payments and how much will he pay in interest? What is the annual percentage rate for this loan?
A couple can afford $400 a month in mortgage payments. How much can they borrow on a 25-year mortgage at 7.2% compounded monthly? How much interest will they pay? What is the annual percentage rate for this mortgage?
How long would it take to pay off a loan of $5,000 at 4.8% compounded monthly making monthly payments of $50 a month? Find the total interest paid on this loan and the annual percentage rate for this loan. You'll need to set up a mathematical model with the present value as an input and the monthly payment as a calculated output value. For your mathematical model, just pick some arbitrary value for the number of years. For example, you might set the number of years to 5. Once your model is complete, you can use the Goal Seek tool to set the monthly payment to $50 by changing the number of years.
You can check your work by looking at my competed workbook: LoansLab01Answers.xlsx