

In the previous Excel project, you learned how to use Excel's COUNTIF function:
=COUNTIF(range, condition)
This function returns the number of values in the specified range of cells that satisfy the given condition.. For example, the Excel expression below counts the number of cells in the range A1 to A60 (inclusive) that contain values equal to the value in cell C5.
=COUNTIF(A$1:A$60, "="&C5)
This function is very helpful but limited by the fact that you can only specify one condition. When generating a grouped frequency distribution, we need a function that allows us to specify two conditions. Specifically, we need to count the number of cells in a specified range that contain values greater than or equal to the lower bound of an interval (the first condition) and, at the same time, less than the upper bound of the interval (the second condition).
Excel's COUNTIFS function allows us to do just that:
=COUNTIFS(range, condition1, range, condition2)
This function returns the number of values in the specified range that satisfy both conditions at the same time. The following expression counts the number of cells in the range A1 to A100 that contain values greater than or equal to the value in cell C4 and less than the value in cell C5:
=COUNTIFS(A$1:A$100, ">="&C4, A$1:A$100, "<"&C5)
(The COUNTIFS function is very powerful. The range of cells can be different for each condition, though all of the ranges must be of exactly the same size and shape. I've illustrated the use of the function for two conditions, but the function can include up to 127 conditions.)
Download and open the file FreqDist02.xlsx. Remind me how.
The sheet titled "Verbal" contains 200 verbal aptitude scores in column A.
1. If you examined this list, you would find that the smallest value is 361 and the largest is 780. An ungrouped frequency distribution (like we created in the previous lab exercise) would require us to list all 420 possible verbal aptitude scores from 361 up to and including 780. The majority of these possible values would have a frequency of zero and the rest would have very small frequencies. Neither the frequency distribution table nor the column chart would help us understand the distribution of verbal aptitude scores.
In situations like this, a grouped frequency distribution is used to illustrate the data (rather than an ungrouped frequency distribution). The possible values are grouped into a number of intervals (of equal size) and the number of data values in each interval is counted. That is, each frequency corresponds to the number of data values within the corresponding interval rather than the number of times a particular value occurs in the data set.
![]() Read
the next section carefully and don't enter anything into your spreadsheet until
you are told to do so. Generating a frequency distribution requires some
preparation and this section describes the basic process.
Read
the next section carefully and don't enter anything into your spreadsheet until
you are told to do so. Generating a frequency distribution requires some
preparation and this section describes the basic process.
Up until now, you have worked with ungrouped frequency distributions and illustrated them using column charts (also called bar charts). Each frequency corresponded to the number of occurrences of a specific value in the data set. There are too many different values in this data set to use that approach. Instead, we will create a grouped frequency distribution. Each frequency corresponds to the number of data elements within a range (or interval) of specific values.
The interval widths are chosen so that there will be about six to fifteen intervals. An approximate value for the interval width can be found by subtracting the minimum value from the maximum and dividing the result by the number of intervals you want. Suppose we want to divide the verbal aptitude scores into about 10 intervals. The approximate interval width is (max - min)/10 = (780 - 361)/10 = 41.9. As a general rule, things are easier if the interval width is an integer. In this case, let's choose an interval width of 40.
The first interval is chosen so that it includes the minimum value in the data set (361, in this case). The specific choice is somewhat arbitrary. Here are some possibilities: 360 to 400, 350 to 390, 340 to 380, and 330 to 370. There are lots of other possibilities (such as 333 to 373) but the four that I listed all include the minimum value of 361 and have boundary values that are nice easy numbers to work with. Let's choose the interval from 330 to 370 as our first interval.
Next, you work your way up creating intervals of size 40 until you reach an interval that includes the maximum value in the data set: 330 to 370, 370 to 410, 410 to 450, 450 to 490, 490 to 530, 530 to 570, 570 to 610, 610 to 650, 650 to 690, 690 to 730, 730 to 770 and, finally, 770 to 810. The final interval (770 to 810) contains the maximum verbal aptitude score of 780
Each interval has a width of 40. The first interval includes all values greater than or equal to 330 and less than 370 and has a midpoint of 350 (halfway between 330 and 370. The second interval includes all values greater than or equal to 370 and less than 410 with a midpoint of 390 (half way between 370 and 410). And so on.

2. On the worksheet, each interval will be represented by its midpoint. Enter the midpoints of the intervals starting in cell C4:
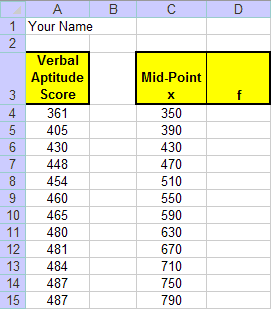
To count the number of values in the first interval (with a midpoint of 350), we could use this formula:
=COUNTIFS(A$4:A$203, ">="&330, A$4:A$203, "<"&370)
This function returns the number of cells in the range A4 to A203 that contain values that are greater than or equal to 330 and, at the same time, less than 370. However, since this formula uses specific numbers (330 and 370) instead of cell references, we can not just simply copy this formula down the rest of the column. Since each interval has different endpoints, we would have to manually enter the endpoints into the formula for each interval.
Notice, however, that given the midpoint of an interval, the endpoints can be found by simple arithmetic. The lower endpoint of the interval is the midpoint minus half the width of the interval and the upper endpoint of the interval is the midpoint plus half the width of the interval. For example, the midpoint of the first interval is 350 and the width of each interval is 40. The lower endpoint of the first interval is 350 - 20 (the midpoint minus half the width of the interval) or 330. The upper bound is 350 + 20 or 370. To count the number of values in the first interval we could use this formula:
=COUNTIFS(A$4:A$203, ">="&(midpt - half width)", A$4:A$203, "<"&(midpt + half width)")
where midpt is the midpoint of the interval and half width is half the width of the interval. The midpoint of the first interval is 350 and half the width of the interval is 20:
=COUNTIFS(A$4:A$203, ">="&(350-20), A$4:A$203, "<"&(350+20))
This doesn't really help since each interval has a different midpoint. So if we copied this formula down the column, we'd have to manually change the midpoint values in each row. However, the midpoint can be represented by a cell reference. The midpoint for the first interval is in cell C4. Consequently, we can modify our formula as follows:
=COUNTIFS(A$4:A$203, ">="&(C4-20), A$4:A$203, "<"&(C4+20))
3. Now you are ready to count the number of values in each interval. Enter the last COUNTIFS function (immediately above) into cell D4. You should get a frequency of 1. Drag the fill handle down the rest of the column. Center align the values in both columns of the table. Use the Auto Sum tool to find the sum of the frequencies (at the bottom of the frequency column). Here is what you should get:
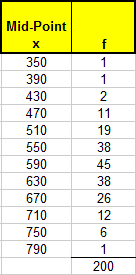
When charting a grouped frequency distribution, a histogram is used instead of a column chart. A histogram is a column chart with no gaps between the columns. Follow the steps below, to generate a histogram illustrating the distribution of verbal aptitude scores.
1. Highlight the frequencies and generate an ordinary column chart.
2. Use the midpoint x values as the category (x) axis labels.
3. Set the chart title to "Distribution of Verbal Aptitude Scores", the x-axis title to "Score", and the y-axis title to "Frequency". Since you are charting only one set of data, there should be no legend.
4. To convert the column chart to a histogram, double-click on one of the columns (it doesn't matter which one) to open the Format Data Series dialog. You can also right-click on one of the columns and choose the Format Data Series option:
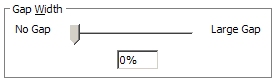
In the Format Data Series dialog, set the gap width to zero percent (no gap).
Then, click the Border Color button and set the border to a solid black line:
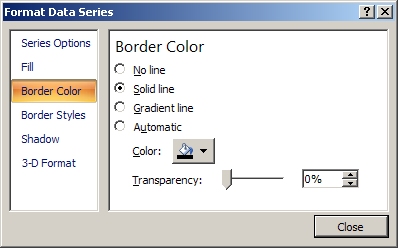
Click the Close button to close the dialog. Click somewhere to the left of the chart to deselect the columns.
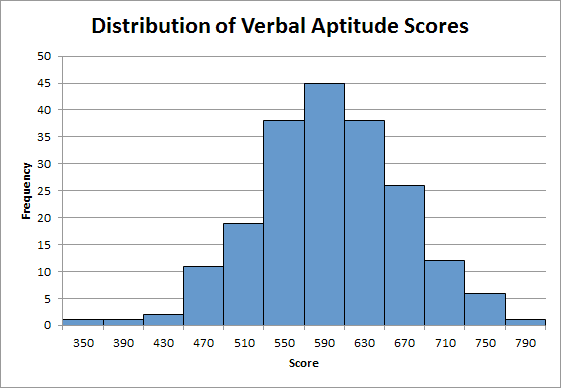
Your final chart should look like the one below Notice that the data appears to be normally distributed.
The sheet titled "Math" contains 200 math aptitude scores in column A. Generate a grouped frequency distribution for this data and illustrate your distribution with a histogram. Set the chart title to "Distribution of Math Aptitude Scores", the x-axis title to "Score", and the y-axis title to "Frequency". Does the distribution appear to be approximately normal?
When you are done, you can check yourself by looking at my answers.
The sheet titled "IQ" contains 300 IQ scores in column A. Generate a grouped frequency distribution and generate a histogram to illustrate your frequency distribution. Set the chart title to "Distribution of IQ Scores", the x-axis title to "IQ", and the y-axis title to "Frequency". Since you are charting only one set of data, there should be no legend. Does the distribution appear to be approximately normal?
When you are done, you can check yourself by looking at my answers.
Each student in a group of MAT 120 students was asked to write down his or her age in months with the following results: 223, 223, 232, 230, 275, 243, 226, 269, 218, 242, 241, 227, 222, 218, 222, 231, 262, 219, 226, 221, 240, 217, 281, 237, 217, 218, 227, 226. On the sheet titled "Ages", generate a frequency distribution using intervals of width 10 with the first interval centered on 220. Illustrate your distribution with an appropriate chart.
Each student in a group of MAT 120 students was asked to write down his or her ideal weight in pounds with the following results: 120, 120, 150, 165, 150, 180, 185, 120, 135, 200, 140, 160, 150, 165, 100, 180, 170, 190, 130, 130, 115, 152, 150, 165, 180, 160, 160, 110 . On the sheet titled "Weights", generate a frequency distribution using intervals of size 15 with the first interval centered on 105. Illustrate your distribution with an appropriate chart.
Here is my completed worksheet: FreqDist02Done.xlsx