

A candy manufacturer has 500 lb. of chocolate, 100 lb. of nuts, and 50 lb. of fruit in inventory. She produces three types of candy. A box of type A requires 3 lb. of chocolate, 1 lb. of nuts, and 1 lb. of fruit and sells for $50. A box of type B requires 4 lb. of chocolate and 1 lb. of nuts and sells for $30. A box of type C requires 5 lb. of chocolate and sells for $20. Assuming she can sell all the candy she makes, how many boxes of each type of candy should she make in order to maximize her income? What is the maximum income?
Here is the mathematical model:
Type Boxes Type A Type B Type C Constraint
A x1 Chocolate: 3x1 + 4x2 + 5x3 ≤ 500
B x2 Nuts: x1 + x2 + ≤ 100
C x3 Fruit: x1 ≤ 50
Income: 50x1 + 30x2 + 20x3 Maximize
Non-Negative: x1, x2, x3 ≥ 0
Introduce slack variables and rewrite the income equation to derive the alternate mathematical model:
Chocolate: 3x1 + 4x2 + 5x3 + s1 = 500 Nuts: x1 + x2 + s2 = 100 Fruit: x1 + s3 = 50 Income: -50x1 - 30x2 - 20x3 + I = 0 Non-Negative: x1, x2, x3, s1, s2, s3, I ≥ 0
Find the optimal solution using the simplex algorithm:
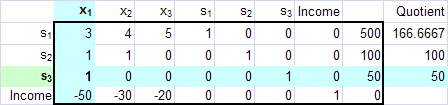
The pivot element is already one so we can move immediately to row operations that will make the remaining values in the pivot column equal to zero.
*row+(-3, [A], 3, 1)*row+(-1, Ans, 3, 2)
*row+(50, Ans, 3, 4)
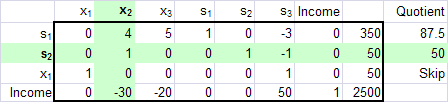
Again, the pivot element is already 1.
*row+(-4, Ans, 2, 1)*row+(30, Ans, 2, 4)
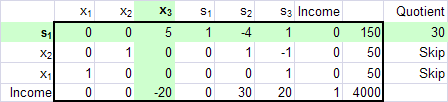
*row(.2, Ans, 1)*row+(20, Ans, 1, 4)
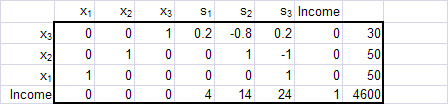
The maximum income is $4,600 when the candy manufacturer makes 50 boxes of type A candy, 50 boxes of type B candy, and 30 boxes of type C candy.
Here is how I set up my Excel solver tool solution:

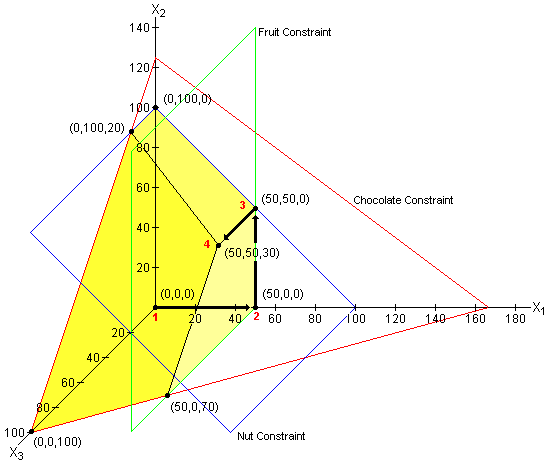
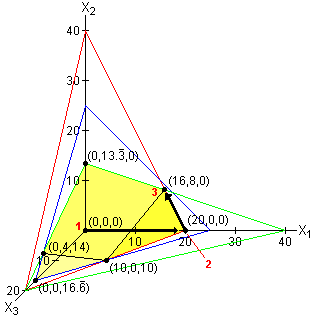
In the illustration below, the plane defined by the red lines represents the chocolate constraint. The plane defined by the blue lines represents the nuts constraint. This plane is parallel to the x3 axis. The plane defined by the green lines represents the fruit constraint. This plane is parallel to both the x2 axis and the x3 axis.
The feasible region extends outward from the origin (towards the viewer) and is bounded by the yellow faces. The simplex algorithm visited four feasible solutions: the origin where the income is $0, the solution (50,0,0) where the income is $2,500, the solution (50,50,0) where the income is $4,000 and, finally, the solution (50,50,30) where the income is $4,600 (the maximum possible).
A small business mass-produces three types of decorative wooden sculptures. Sculpture A requires 4 hours to cut the wood, 2 hours to assemble, and 1 hour to apply the finish and it sells for $500. Sculpture B requires 2 hours to cut the wood, 2 hours to assemble, and 3 hours to apply the finish and it sells for $300. Sculpture C requires 4 hours to cut the wood, 3 hours to assemble, and 2 hours to apply the finish and it sells for $400. There are two employees who cut the wood, one who assembles the sculptures, and one who applies the finish. Each worker can work, at most, 40 hours a week except the assembler who can work 50 hours a week. How many of each type of sculpture should be made each week in order to maximize the revenue? What is the maximum revenue?
Here is the mathematical model for this problem.
Type Number Type A Type B Type C Constraint
A x1 Cutting: 4x1 + 2x2 + 4x3 ≤ 80
B x2 Assembly: 2x1 + 2x2 + 3x3 ≤ 50
C x3 Finish: x1 + 3x2 + 2x3 ≤ 40
Revenue: 500x1 + 300x2 + 400x3 Maximize
Non-Negative: x1, x2, x3 ≥ 0
Introduce slack variables and rewrite the revenue equation to derive the alternate mathematical model:
Cutting: 4x1 + 2x2 + 4x3 + s1 = 80 Assembly: 2x1 + 2x2 + 3x3 + s2 = 50 Finish: x1 + 3x2 + 2x3 + s3 = 40 Revenue: -500x1 - 300x2 - 400x3 + R = 0 Non-Negative: x1, x2, x3, s1, s2, s3, R ≥ 0
Find the optimal solution using the simplex algorithm:
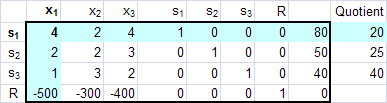
*row(.25, [A], 1)*row+(-2, Ans, 1, 2)
*row+(-1, Ans, 1, 3)
*row+(500, Ans, 1, 4)
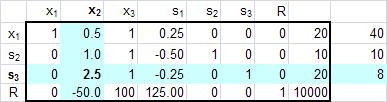
*row(.4, Ans, 3)*row+(-.5, Ans, 3, 1)
*row+(-1, Ans, 3, 2)
*row+(50, Ans, 3, 4)
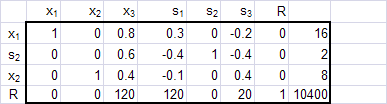
The maximum Revenue is $10,400 when 16 type-A sculptures, 8 type-B sculptures, and no type-C sculptures are made. Each employee will work 40 hours except the assembler who will work 48 hours (the slack variable for the assembly constraint is 2 hours).
Here is how I set up my Excel solver tool solution:

In the illustration below, the feasible region is a three-dimensional region extending out from the origin (towards the viewer) and bounded by the three shaded faces. Each edge is formed by two intersecting planes and each vertex is at the intersection of three planes. These vertices correspond to the feasible solutions to this system and the maximum profit will occur at one of them. The simplex algorithm visited three of these vertices. The initial simplex tableau corresponds to the origin (P = 0). The second vertex was the basic solution at (40,0,0) where P = 10,000. The final vertex was at (16,8,0) where the maximum value of P is achieved (P = 10,400).
On average, an adult male under the age of 50 requires at least 32 grams of fiber per day and at least 60 grams of protein. A survivalist has a supply of two types of dietary supplements. The type-A supplement is 20% fiber and 50% protein (by weight). The type-B supplement is 32% fiber and 30% protein (by weight). How many grams of each type of supplement are needed to satisfy the minimum daily requirements for fiber and protein if the total weight is to be as small as possible?
Here is the mathematical model for this problem.
Type Grams Type A Type B Constraint
A x1 Fiber: 0.2x1 + 0.32x2 ≥ 32
B x2 Protein: 0.5x1 + 0.30x2 ≥ 60
Total: x1 + x2 Minimize
Non-Negative: x1, x2 ≥ 0
Set up the matrix representation of this system and find the transpose:
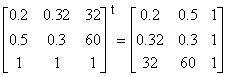
Use the transpose to formulate the dual problem:
0.20y1 + 0.5y2 ≤ 1
0.32y1 + 0.3y2 ≤ 1
y1, y2 ≥ 0
Maximize P = 32y1 + 60y2
Introduce slack variables into this dual problem:
0.20y1 + 0.5y2 + x1 = 1
0.32y1 + 0.3y2 + x2 = 1
-32y1 - 60y2 + P = 0
y1, y2, x1, x2 ≥ 0
Solve the dual problem using the simplex algorithm:
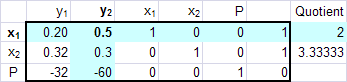
*row(2, [A], 1)*row+(-0.3, Ans, 1, 2)
*row+(60, Ans, 1, 3)
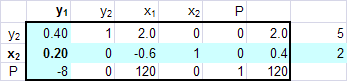
*row(5, Ans, 2)*row+(-.4, Ans, 2, 1)
*row+(8, Ans, 2, 3)

The solution to the minimization problem can be read from the bottom row of the final tableau. The minimum total mass is 136 grams when 96 grams of type-A supplement is used and 40 grams of type-B supplement is used.
In the graph below, the red line represents the fiber constraint (0.2x1 + 0.32x2 ≥ 32) and the green line represents the protein constraint (0.5x1 + 0.3x2 ≥ 60). These lines cross at the point (96, 40).
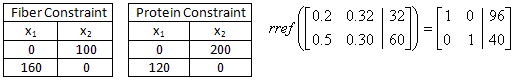
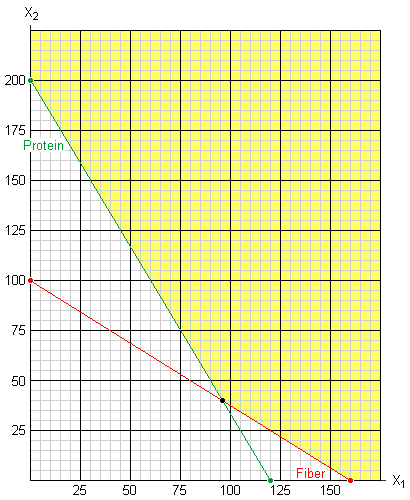
The minimum is at one of the vertices: (0, 200), (96, 40), or (160,0). Since the objective function is simply the sum of the two coordinates, it is easy to determine that the optimal solution is at (96, 40) with a total weight of 136 grams.
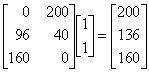
Here is how I set up my Excel solver tool solution:
