

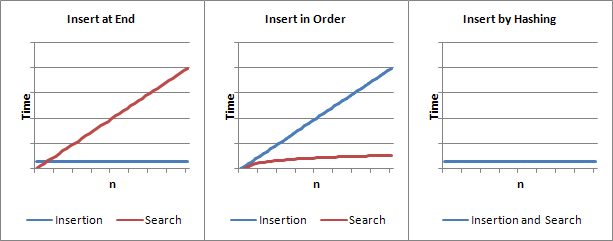
In this assignment, you will investigate a data structure and associated algorithms that allow constant time searches. That is, the time required to search for a particular element is the same whether the data structure is almost empty or almost full.
Consider a statically allocated array of records in which each record has a key field with a unique value (i.e., no two records have the same key value). The fasted way to insert a new record is to place it into the next available slot. However, to search for a particular record by its key value, we would need to implement a linear search algorithm. While, insertion into the list can be done in constant time, a search would require linear time.
Another approach would be to insert new records into the array in sort order based on the value of the key field. In that case, insertion would require linear time but a binary search could be used requiring only log(n) time.
A hash table is basically a statically allocated array in which insertions are done in such a way that both inserting a new record and searching for an existing record require constant time. The array index for a given record is determined by a function that converts the key value of the record into a valid array index. This calculation is performed to determine where to insert a new record. This calculation is done again when searching for a record having a specific key value. The program then checks the corresponding slot in the array to see if the target record is there. Since the function to convert a key value into an array index runs in constant time, inserting a record and searching for a record require only constant time.
Here is a visual comparison of the insertion and search times of these three methods:
The function that converts a key value to a valid array index is called a hashing function. As an example, let's think about a function that converts a string value to a valid array index. You could begin by finding the sum of the character codes as an unsigned integer. Then, take this unsigned integer value and divide it by the size of the array. The remainder will be a valid array index since division by n results in a remainder in the range 0 to n-1.
Suppose we want to convert "Computer Science" into a valid array index for an array of size 101:
![]()
A record whose key value was "Computer Science" would be inserted into the array at index 62.
Though simple to implement, this is a poor hashing function. The design of a good hashing function is difficult and well beyond the scope of this assignment (though we will consider a better algorithm below).
As you would expect, there are some downsides to this blazingly fast search capability. Since the location of a record is calculated by the hashing function, there is generally a gap in the array between one record and the next. This makes a linear traversal a bit more difficult. In effect, you have to traverse the entire array (even if there are only a few records in it) and process only those slots in which records have actually been stored. This implies that there is some way to determine that a slot is not currently being used to store valid data.
The records in a hash table cannot be sorted. Sorting an array results in the records being rearranged (i.e., moved to different slots). If you move records to different slots then the hashing function can no longer be used to determine the location of the corresponding record.
In general, hash tables work best if they are not too full. Consequently, you should allocate more space than the largest data set would require.
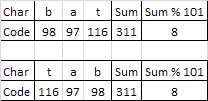
What, you might ask, is to prevent the hashing function from mapping two different strings to the same array index? Nothing. Given the hashing function described above, it should be obvious that "bat" and "tab" would both map to the same location in the array (index 8):
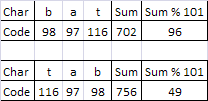
Mapping two records to the same index is called a collision. Such obvious collisions as "bat" and "tab" can be avoided by modifying the hashing function. For example, in the for loop that calculates the sum of the codes you can replace "sum = sum + code" with "sum = 2*sum + code". That is, the new sum is twice the old sum plus the next character code. You may recall that this is the same basic idea that we used before when converting a text representation of an integer into an integer value (value = 10*value + digit). Here is what we would get for "bat" and "tab" using this improved hashing function:
However, even with an improved hashing function, collisions will occur and are more likely as the table becomes nearly full. Every hash table must implement a collision handling algorithm. One way to handle collisions is to create the hash table as an array of linked lists. When a new record is mapped to a specific index, it is simply added to the head of the corresponding linked list.
This approach has the advantage that it actually allows you to store more records in the hash table than there are slots. For example, in a hash table with 101 linked lists, you could store 202 records with an average of only 2 records in each linked list. To search for an item, you determine the index at which the item should be found (using the hashing function) and then traverse the corresponding linked list until you find the item or reach the end of the list.
Like our other data structures, a hash table will be defined as a template class. That is, it will be able to store items of any type. This flexibility leads to problems. The hash table has no way of identifying the key field of the objects being stored. Consequently, it can not know how to convert the corresponding key values to valid array indexes nor can it perform a search (which is based on comparing key values).
The solution to the hashing problem is to require that each object be able to convert its key value into an unsigned integer. That is, we require that the object's class include a member function (named hashcode) that converts a key value to an unsigned integer. The hash table asks the item to return its hashcode and then divides it by the number of slots in the table. The resulting remainder is the array index for that item. In effect, the item does the integer conversion part and the hash table carries out the appropriate division.
We also require that each item in the list be able to compare its key value with the key value of another item of the same type. That is, we require that the item's class definition include a member function (named key_equal) that returns true if the key value of the invoking item is equal to the key value of a second item of the same type.
These prerequisites mean that we cannot store simple data types in a hash table. But why would we want to do that anyway? The whole point of a hash table is to be able to insert and search for a record based on the value of its key field.
You are to write a program that reads a text file and generates a table of the words found in the file and the number of times each word was found. For the purposes of this assignment, a word will be defined as a whitespace-delimited sequence of characters. This is precisely how the extraction operator extracts strings from the input stream. When extracting a string value, extraction begins with the first non-whitespace character. Extraction continues until a whitespace character is encountered. That whitespace character is not extracted from the stream.
In this assignment, words are not case-sensitive. For example, "The" and "the" are the same word. Consequently, I suggest that when you read a word from the input file, you immediately convert it to lowercase.
The output is to be written to a text file in the form of a table with two columns. The first column contains the words found in the input file and the second column contains the corresponding frequencies. The words are to be listed in alphabetical order (see sample output).
The user will specify the name of the text file that the program is to process. The text that produced the sample output referred to above is Mary Had a Little Lamb. To give your program a more vigorous workout, you might give it the Rime of the Ancient Mariner to process.
Read the text file one word at a time. A word is a sequence of characters that begins with a letter of the alphabet and contains only letters of the alphabet and apostrophes (to allow for contractions such as "isn't"). For each word, search the table to see if the word is already in the table. If it is, increment its frequency. Otherwise, insert the word into the table with a frequency of one.
When you are done, perform a linear traversal of the hash table adding each token to a list, sort the list alphabetically, and write the words and corresponding frequencies to the output file. Display a message on the screen telling the user how many distinct words were found (the size of the list) and where to find the output.
Write a template class that implements a hashTable as a dynamically allocated array of linked lists. The default constructor should create an empty hash table of size 53. An initialization constructor should create a hash table with the size specified by its only parameter. The destructor should return all of the memory allocated for the table back to the operating system. This includes the memory allocated for the dynamically allocated array itself and the memory allocated for each list in the array of lists.
You should also include a member function to:
Implement a tokenType class that has two data members: a string value (the key field), and an integer value (the frequency). This class must implement a hashing function named hashcode that converts the text value of the object that invokes this function into an unsigned integer value.
The tokenType class must also include a function named key_equal. This function has one parameter which is a tokenType object and the function returns true if the key of the invoking token equals the key of the token parameter.
You will also need to implement the less than (<) and is equal to (= =) operators. Both should be based on the tokens' text values.
In general, the key_equal function and the == operator will be based on different things. For example, we might have said that two tokens are equal (==) if the two text fields are the same and the two frequencies are the same. The key_equal function is used by the hashTable class and the == operator is used by the list class.
Use your implementation of a singly-linked list in this project. You can use the implementation you created for Homework 5.
I've done some of the grunt work for you in Lab06.cpp. Submit your completed Lab06.cpp file as an email attachment.