Given an investment of $3,000 at 5% compounded quarterly for 6 years, find the interest earned and the future value.
i = r/ppy = .05/4 = 0.0125
n = t * ppy = 6 * 4 = 24
A = P(1+i)n = 3000(1.0125)24 = $4,042.05
3000
1.0125
24
4,042.05
I = A - P = 4042.05 - 3000.00 = $1,042.05
Using the TI-83 TVM Solver
The TI-83 calculator includes an application called TVM Solver (Time Value of Money) that allows you to solve problems like these without using the formulas directly (they are a part of the application itself). To activate the TVM Solver application, press the following buttons:
Pressing the
button displays the application menu. The first application listed (Finance) is
the default selection so all you have to do is press the
button. The default option in the finance menu is the TVM Solver so, again, all
you need to do is press the
button.
The TVM Solver screen displays eight lines as follows:
| Variable | Purpose |
| N | The total number of periods |
| I% | The nominal annual rate entered as a percent |
| PV | The present value |
| PMT | The periodic payment |
| FV | The future value |
| P/Y | The number of payment periods per year |
| C/Y | The number of compounding periods per year |
| PMT: | Indicates whether payments are made at the end or the beginning of the each payment period |
Normally, the number of payment periods is the same as the number of compounding periods. Consequently, the value that you enter for P/Y is copied as the value of C/Y. However, you can manually alter the value of C/Y if necessary. For example, if you were making quarterly payments into an account with monthly compounding, you would enter 4 as the number of payment periods per year and then enter 12 as the number of compounding periods per year. This type of problem cannot be solved using the basic formulas given in our text.
Enter the following values in the TVM Solver window:
N=24 I%=5 PV=3000 P/Y=4
In the TVM Solver window, move the cursor back up to the FV variable and
press the buttons:
.
The future value will be given as -4042.053151. In the TMV Solver, positive
values represent cash inflows and negative values represent cash outflows. The
present value represents a cash inflow into this investment and was entered as a
positive value. The future value is shown as a negative because it represents
the amount of money that you could withdraw from the investment at the end (a
cash outflow).
Redo example one above assuming that the interest is compounded monthly instead of quarterly.
i = r/ppy = .05/12 = 0.004166666...
Since the periodic rate is a repeating decimal, we will calculate it as part of the future value calculation. We do not simply round this value off and use it. That would lead to inaccurate results.
n = t * ppy = 6 * 12 = 72
A = P(1+i)n = 3000(1 + 0.05/12)72 = $4047.05
3000
1
.05
12
724,047.05
I = A - P = 4047.05 - 3000.00 = $1,047.04
Using the TI-83 TVM Solver
Changing the number of periods per year to 12 changes the total number of periods to 72. Consequently, you'll need to change the values of N and P/Y:
N=72 I%=5 PV=3000 P/Y=12
Move the cursor to the FV variable, and press
.
Find the present value of an investment if the future value is $1,000. The investment pays 4.5% compounded semiannually for seven years.
i = r/ppy = 0.045/2 = 0.0225
n = t * ppy = 7 * 2 = 14
P = A(1+i)-n = 1000(1.0225)-14 = $732.34
10001.0225
14732.34
Using the TI-83 TVM Solver
Set the TVM variables as follows:
N=14 I%=4.5 FV=1000 P/Y=2
Move the cursor to the PV variable and press
.
Tom loaned Sally $3,000 with the understanding that she would pay him back $3,600 in three years. What is the nominal annual interest rate assuming that interest is compounded monthly?
nn = t * ppy = 3 * 12 = 36
Solve the equation A = P(1 + i)n for i:
The nominal annual rate is the periodic rate multiplied by the number of periods per year:
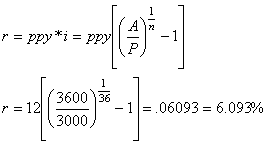
1236003000136
10.060928006
Using the TI-83 TVM Solver
Set the TVM variables as shown below. Remember to use the negation button
rather than the subtraction button
when entering the future value.
N=36 PV=3000 FV=-3600 P/Y=12
Move the cursor to the I% variable and press
.
How long will it take an investment of $200 to amount to $250 at 6% compounded quarterly?
i =.06/5 = 0.015
Solve the equation A = P(1 + i)n for n:
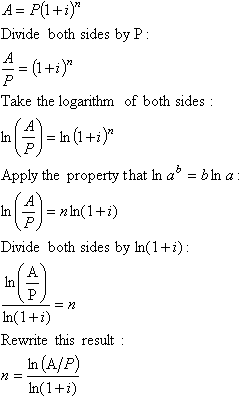
Note: In the derivation, I took the natural logarithm of both sides. I could also have taken the common logarithm of both sides. Plugging in the values in our example we get:
The value of n generated by this technique should always be rounded up to an integer value since interest is only paid at the end of a period. In this case, the future value after 15 quarters ($250.05) will be slightly higher than the target value of $250 but the future value after only 14 quarters ($246.35) would be too low.
On the TI-83, tapping the
button automatically displays the opening parenthesis for the function argument.
You must remember to include the closing parenthesis as illustrated here:
2502001.01514.98753167
Here is what is displayed on the TI-83 screen after typing the keystrokes up
to but not including the
key:
When you tap the enter key, the result appears on the next line of the display.
Using the TI-83 TVM Solver
Set the TVM variables as follows:
I%=6 PV=200 FV=-250 P/Y=4
Move the cursor to the N variable and press
.