

Excel provides a function named PV that can be used to calculate the future value of a one-time investment or the future value of an annuity:
=PV(rate, nper, pmt, [fv], [type])
The rate argument is the periodic rate, nper is the total number of periods, and pmt represents the periodic payment. If you are trying to find the present value of a one-time investment then the value of the pmt argument is zero since there are no periodic payments. Typically, the pmt argument is a negative value since it represents an expense (income is positive and outflow is negative).
The last two arguments are optional. This is indicated by the square braces that surround each argument. The fv argument represents the future value. For an annuity, the value for fv is typically zero. For a one-time investment, fv represents the future value of the investment. The type argument indicates whether the annuity is an ordinary annuity with payments made at the end of the period (type = 0) or an annuity due with payments made at the beginning of the period (type = 1). For the present value of an ordinary annuity, you can just omit the last two arguments because the default value for each is zero.
1. Download and open the file, Lab03.xlsx. Remind me how. Enter your name in cell B1 of the amortization sheet.
2. A business woman calculates that she can make payments of $1,750 a month on a loan to help her start her business. Suppose that the term of the loan is ten years and that she is charged 7.3% compounded monthly. How much money can she borrow and how much interest will she pay on the loan? Begin by entering these initial data values on the worksheet.
3. Enter appropriate formulas for the periodic rate and the number of periods.
4. Find the present value and total interest using formulas.
a. In the present value cell, enter an Excel formula that invokes the PV function. Try to do this on your own. You should get a value of $148,732.96. Help
b. In the cell for the total interest paid, enter an Excel formula to calculate the total interest earned. Remember, the total interest is the difference between what she gets from the investment and what she puts into the investment. This time, because she is paying interest, she will put in more than she gets out. You should get a result of $61,267.04. Help
c. Highlight the cells containing the present value and the total interest by setting the background color to light gray, adding borders around the cells, and setting the font to bold.
5. Following the steps below, prepare an amortization table that shows the status of the loan after each payment. This is done pretty much the same way you did the tables in the previous labs but with a few changes:
a. Recall that fictitious period zero is included to make graphs look nicer. The new balance at the end of period zero is the amount of money borrowed. It represents the amount she owes the bank at the very beginning of the term.
b. The new balance at the end of each period is the initial balance plus the interest that you must pay minus the monthly payment.
c. You should discover that the final balance at the end of the last period is not zero. In fact, it is negative four cents. How do you explain this?
d. In the very last row of the table, you must alter the size of the final payment. Instead of $1,750.00, it should be the sum of the initial balance (the amount she still owes at the beginning of the last period) and the interest she must pay on that amount. Enter the appropriate formula using cell references.
e. Format the financial values in the body of the table (every column but the first) using the comma format.
6. Create a line chart showing how the loan balance declined during the term of the loan.
You can check your work by looking at my workbook: Lab03Done.xlsx
What nominal annual interest rate would allow our business woman to borrow $150,000 with monthly payments of $1,750 for ten years. Given fixed payments, the only way the present value can go up is if the interest rate goes down. We would anticipate, then, that the interest rate would be less than the 7.3% she was paying above.
To find the nominal annual rate, we have to solve the present value formula for the periodic rate. Unfortunately, that is not possible. Nevertheless, Excel provides a way for you to determine the answer to the question. It is called the "Goal Seek" tool. This tool allows you to set the value of a given cell to a particular value by changing the value in some other cell. In this case, you want to change the value of the present value to 150,000 by changing the nominal annual rate.
1. Click on the cell that contains the present value of the loan.
2. Click on the Data tab near the top of the workbook. In the data tools section, click on the What-if Analysis tool. Finally, click on the Goal Seek option. The Goal Seek dialog window will appear:
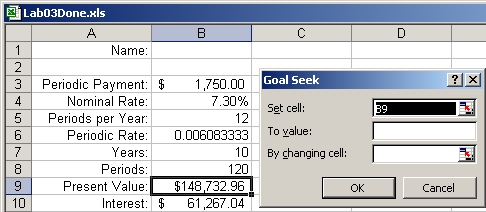
3. Be default, the cell whose value is to be set is the cell that was selected when the Goal Seek tool was activated. That is why we selected the present value cell before activating the tool. If the selected cell is not the cell whose value is to be set, then you can select proper cell by typing in its cell address or by clicking on the cell itself.
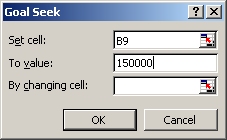
4. Type the value you want to appear in this cell in the text box labeled To value. In this case, the value is 150000:
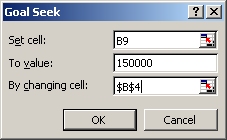
5. Finally, you need to specify the cell whose value needs to be changed in order to achieve the goal that you have just indicated. Click in the text box labeled By changing cell and either type in the address of the nominal rate cell or click on the cell itself. If you click on the cell, Excel will display its address using absolute references but they are not needed if you just type it in:
6. Click the OK button. A Goal Seek Status window will appear indicating whether the goal seek operation was successful or not. In this case, it will be:
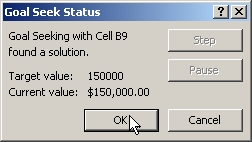
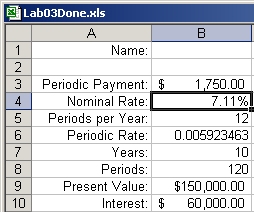
7. Click the OK button to close this window. If you look at your worksheet, you'll notice that the nominal rate has been changed to 7.11% (displayed to two decimal places) and that the present value is now $150,000 as requested. The value of the periodic rate will also have changed since it is the nominal rate divided by the number of periods. The total interest also changed since it is based on both the nominal annual rate and on the present value. Here is a portion of my worksheet illustrating all of these changes:
Do the lab exercise on the worksheet named "Lab Exercise".
A man wants to borrow $100,000 for twenty-five years in order to buy a house. The bank offers a mortgage at 6.9% interest compounded monthly. How much will the man's monthly payments be and how much interest will he pay? Create an amortization table to show how the loan balance declines over time and generate a line chart to illustrate this decline.
As you did in the previous lab (Lab02), you will need to use Excel's PMT function to find the periodic payment.