

Consider this system of linear equations:
Supply: 10p - 4q = 32 Demand: 11p + 19q = 170
In this system, p represents the price of an item in dollars and q represents the quantity in hundreds. The first equation describes the relationship between price and quantity from the perspective of the supplier. The second equation describes the relationship from the perspective of the consumer. Our goal is to solve this system of equations simultaneously.
1. Download and open the file, Lab04.xlsx. Remind me how. Enter your name in cell B1 of the supply & demand worksheet.
2. The worksheet has been set up as shown here:
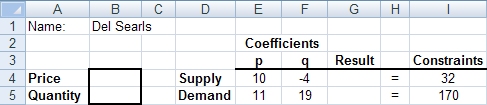
You'll notice that this looks a lot like the setup we use when solving this kind of problem by hand or when using the TI-83 calculator. The cells B4:B5 will eventually be used to display the solution to the system of equations.
3. In cell G4, write an Excel formula that will generate the result for the expression10p - 4q where the value of the price (p) is in cell B4 and the value of the quantity (q) is in cell B5. For the coefficients (10 and -4), use appropriate cell references (E4 and F4, respectively) instead of the actual numbers. You should get a value of zero since, at this point, there are no values in either B4 or B5. If a cell is empty, Excel interprets it as a zero.
4. In cell G5, write an Excel formula that will generate the result 11p + 19q where the value of the price is in cell B4 and the value of the quantity is in cell B5. Use the appropriate cell references for the coefficients 11 and 19. Again, you should get a value of zero.
5. To double-check your formulas, enter a price of 5.5 in cell B4 and a quantity of 6 in cell B5. Remember that the quantity is in hundreds so entering 6 corresponds to a quantity of 600. These values should yield a result of 31 for the supply equation and a result of 174.5 for the demand equation. If they didn't, you probably made a mistake in cell G4 or G5. If you get stuck, look at the correct formulas.
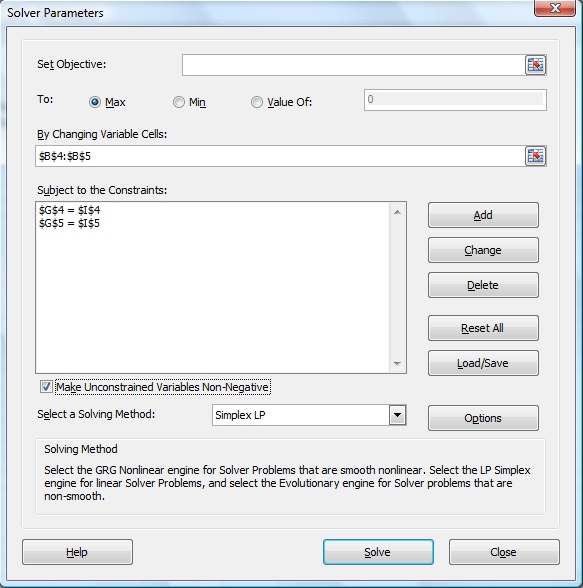
6. To use the Solver tool, click on the Data tab and look in the Analysis group. Select the solver tool. If there is no Solver tool, click on this link: Enabling the Solver Tool
7. Since neither price nor quantity should be negative, check the box with the label "Make Unconstrained Variables Non-Negative". Just below that, select the Simplex LP solving method (since our model consists of linear equations.
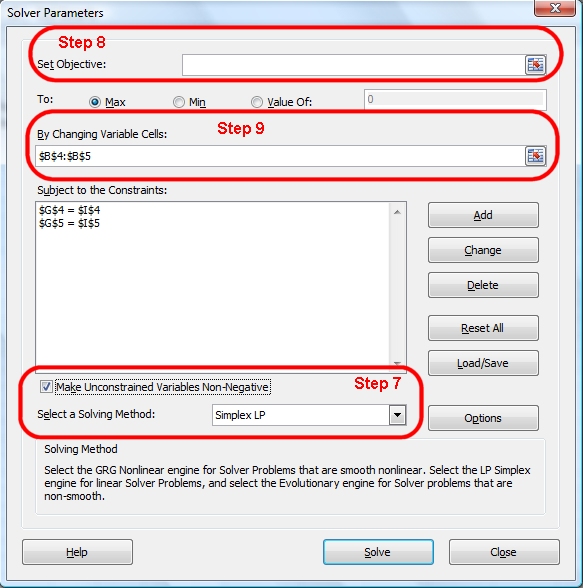
8. If necessary, clear the entry in the Set Objective box at the upper right of the Solver Parameters dialog. See the picture above if you need help.
9. The cells whose values the solver will change are the cells containing the values of price and quantity (the variables in our system of linear equations). Recall the price and quantity are in cells B4:B5. Enter this range of cells in the By Changing Cells box. The easiest way to do this is to make the text box active by clicking in it and then selecting cells B4:B5 using the mouse. See the picture above if you need help.
10. The values of price and quantity are to be changed subject to the constraints that, for each equation, the calculated result (in column G) should be equal to the value in the constraint column (column I). Click the Add button to add a constraint. In the Cell Reference text box, enter the cell reference for the cell that contains the calculated result for the supply equation (cell G4). The easiest way to do this is to make the text box active by clicking in it and then point at the cell that contains the calculated result (cell G4).
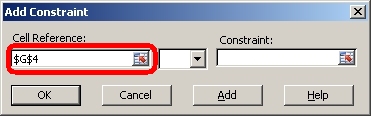
11. In the scroll down menu in the middle, make sure the type of constraint is equality (the equal sign).
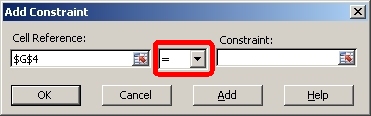
12 In the Constraint text box, enter the cell reference for the cell that contains the constraint value for the supply equation (cell I4). Again, the easiest way to do this is to activate the text box by clicking on it and then clicking on the cell that contains the constraint value (cell I4). When you are done, click the Add button.
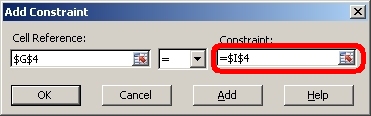
13. Add a second constraint for which the cell reference refers to the result of the demand equation with the constraint that it be equal to the corresponding value in the constraint column. When you are done, click the OK button. The Solver Parameters dialog should look like this:
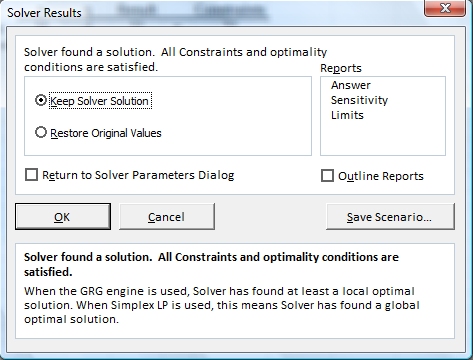
15. Click the Solve button and the Solver Results dialog will be displayed (see image below). Click the OK button to close this dialog window and keep the Solver solution.
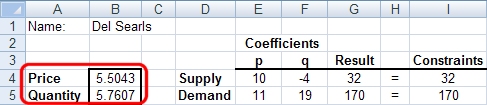
16. Look at the spreadsheet and confirm that the values in the results column are the same as the corresponding values in the constraints column. To achieve these results, the quantity is 576 (to the nearest integer) at a price of $5.50 (to the nearest penny):
A company produces Italian sausages and bratwursts at plants in Green Bay and Sheboygan. The Green Bay plant can make 800 sausages an hour and 800 bratwursts an hour. The Sheboygan plant can make 500 sausages and 1,000 bratwursts an hour. How many hours should each plant be scheduled to fulfill an order for 62,250 sausages and 76,500 bratwursts?
1. Activate the Meats worksheet and set up a model for this problem. Make your best effort before you look at my model.
2. Use the Excel Solver tool to determine the number of hours each plant should be scheduled. You should find that the Green Bay plant needs to run for 60 hours and the Sheboygan plant needs to run for 28.5 hours.
A research laboratory technician is able to purchase two brands of animal food having the following compositions: Brand A is 10% protein and 6% fat and brand B is 20% protein and 2% fat. How many grams of each brand should be used to create a mix that has 20 grams of protein and 6 grams of fat?
1. Model this system on the worksheet named "Lab Exercise".
2. Use Excel's Solver tool to determine how many grams of each mix should be used.