

The process for solving an optimization problem in Excel is very similar to the process used to solve a system of linear equations back in Lab 4. When solving a system of linear equations, the calculated results had to equal the constraint values. However, when solving optimization problems, the constraints are inequalities instead.
A furniture manufacturing company manufactures dining room tables and chairs. A table takes 8 hours to assemble and 2 hours to finish. A chair takes 2 hours to assemble and 1 hour to finish. The maximum number of labor-hours per day is 400 for the assembly process and 120 for the finishing process. If the profit on a table is $90 and the profit on a chair is $25, how many tables and chairs should be made each day to maximize the profit (assuming that all of the tables and chairs can be sold)?
The following model was derived in the first example of the Simplex algorithm (where x1 is the number of tables and x2 is the number of chairs):8x1 + 2x2 ≤ 400 (assembly) 2x1 + x2 ≤ 120 (finishing) P = 90x1 + 25x2 x1, x2 ≥ 0 Maximize P
1. Download and open the file, Lab07.xlsx. Remind me how. Put your name in cell B1 of the example 1 worksheet.
2. The model given above has been set up on the first worksheet as illustrated below:
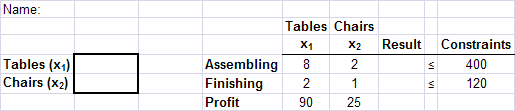
3. In the result column, enter the Excel formulas that will calculate the corresponding results using cell references whenever possible:
Remember that since we have not yet assigned values to the variables in B4:B5, the results will all have a value of zero.
Did you enter the expression =E4*$B$4+F4*$B$5 in cell G4? If so, you were able to copy the formula down the next two rows (into G5 and G6). If you forget to use absolute references, you will get incorrect results.
4. Now for a challenge. Delete the contents of cells G4:G6 (the results column). Instead of writing an expression in cell G4 and copying it down the column, write a single expression that will find all three results at the same time using matrix multiplication. You learned how to use Excel's MMULT function in the computer inventory problem in Lab 05. Do your best to work this out on your own but if you get stuck, here is some help.
5. Activate the solver tool (on the Data tab in the Analysis section).
6. On the Solver Parameters dialog, check the box with the label "Make Unconstrained Variables Non-Negative". Just below that, select the Simplex LP solving method (see the image following step 7).
7. The goal is to maximize the profit. Consequently, we need to set the target cell (G6) to its maximum value by changing cells B4 and B5 subject to our constraints.
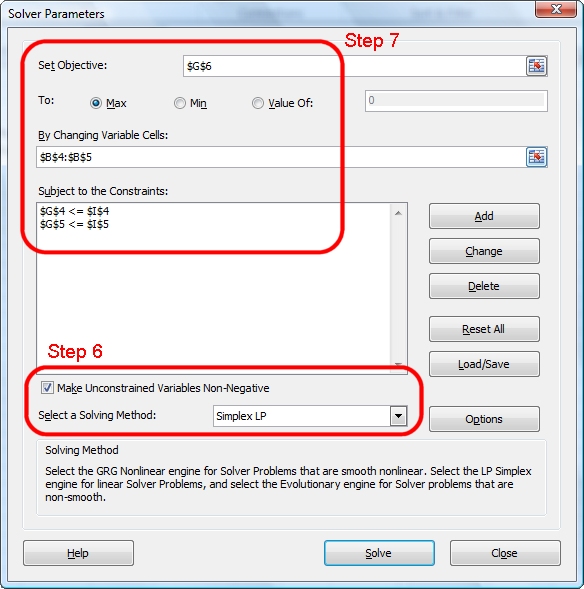
8. Click the Solve button. The Solver generates the optimal solution: x1 = 40 tables, x2 = 40 chairs, P = $4,600. Click the OK button to keep the Solver solution.
A farmer owns a 100-acre farm and plans to plant at most three crops. The seed for crops A, B, and C costs $40, $20, and $30 per acre, respectively. A maximum of $3,200 can be spent on seed. Crops A, B, and C require 1, 2, and 1 workdays per acre, respectively, and there are a maximum of 160 workdays available. If the farmer can make a profit of $100 per acre on crop A, $300 per acre on crop B, and $200 per acre on crop C, how many acres of each crop should be planted to maximize profit?
Here is the mathematical model from the third example of the Simplex algorithm (where x1 is the number of acres of crop A, x2 is the number of acres of crop B, and x3 is the number of acres of crop C):
x1 + x2 + x3 ≤ 100 (available acreage)
40x1 + 20x2 + 30x3 ≤ 3200 (money for seed)
x1 + 2x2 + x3 ≤ 160 {available labor)
P = 100x1 + 300x2 + 200x3
x1, x2 ,x3 ≥ 0
Maximize P
1. On the Example 2 worksheet, set up the mathematical model for this example.
2. Use the Solver tool to maximize the profit given the problem constraints. You should find that x1 = 0 acres of crop A, x2 = 60 acres of crop B, x3 = 40 acres of crop C, and the maximum profit is $26,000.
If you did not get the correct solution, try to find your error. If you get really stuck, try help.
A mining company operates two mines, each of which produces three grades of ores. The West Summit mine can produce 2 tons of low-grade ore, 3 tons of medium-grade ore, and 1 ton of high-grade ore per hour of operation. The North Ridge mine can produce 2 tons of low-grade ore, 1 ton of medium-grade ore, and 2 tons of high-grade ore per hour of operation. To satisfy existing orders, the company needs at least 100 tons of low-grade ore, 60 tons of medium-grade ore, and 80 tons of high-grade ore. If it costs $400 per hour to operate the West Summit mine and $600 per hour to operate the North Ridge mine, how many hours should each mine be operated to supply the needed amounts of ore and, at the same time, minimize the cost of production?
1. Derive a mathematical model for this problem. It is important that you do this for yourself. When you are done, look at my model to make sure that your model is correct.
2. On the Example 3 worksheet, set up the mathematical model for this example.
3. Use the Solver tool to minimize the cost of production given the problem constraints. You should find that x1 = 20 hours, x2 = 30 hours, and the minimum cost of production is $26,000.
If you did not get the correct solution, try to find your error. If you get really stuck, try help.
A small accounting firm prepares tax returns for three types of customers: individual, commercial, and industrial. The tax preparation process begins with a 1-hour interview with the customer. The data collected during this interview is entered into a time-sharing computer system, which produces the customer's tax return. It takes 1 hour to enter the data for an individual customer, 2 hours for a commercial customer, and 1.5 hours for an industrial customer. It takes 10 minutes of computer time to process an individual return, 25 minutes to process a commercial return, and 20 minutes to process an industrial return. The firm has one employee who conducts the initial interview and two who enter data into the computer. The interviewer can work a maximum of 50 hours per week and each of the data-entry employees can work a maximum of 40 hours a week. The computer is available for a maximum of 1,025 minutes a week. The firm makes a profit of $50 on each individual customer, $65 on each commercial customer, and $60 on each industrial customer.
Set up the mathematical model for this problem on the lab exercise worksheet and use the solver tool to determine how many customers of each type the firm should schedule to maximize its profit. What is the maximum profit?