A woman wants to use milk and orange juice to increase the amount of calcium and vitamin A in her daily diet. An ounce of milk contains 37 milligrams (mg) of calcium and 57 micrograms (mcg) of vitamin A. An ounce of orange juice contains 5 mg of calcium and 65 mcg of vitamin A. How many ounces of milk and orange juice should the woman drink each day to provide exactly 500 mg of calcium and 1,200 mcg of vitamin A?
Let x1 represent the number of ounces of milk and x2 the number of ounces of orange juice. Here is a mathematical model of this problem:
Calcium: 37x1 + 5x2 = 500 mg Vitamin A: 57x1 + 65x2 = 1200 mcg
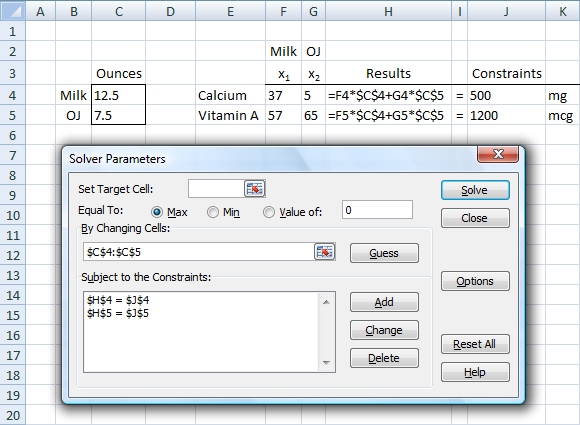
This model was set up in Excel as shown below:
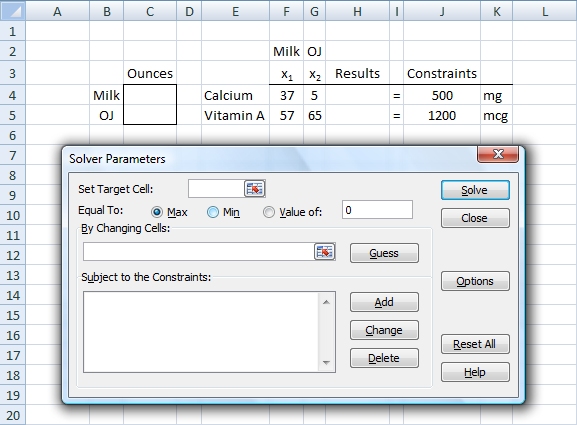
1. What Excel expression should go in cell H4?
The result is the calculated milligrams of calcium: 37x1 + 5x2 = F4*C4 + G4*C5
2. What Excel expression should go in cell H5?
The result is the calculated micrograms of vitamin A: 57x1 + 65x2 = F5*C4 + G5*C5
3. What range of cells should go in the "By Changing Cells" box in the Solver Parameters dialog?
The solver should change the values of x1 and x2 in cells C4:C5.
4. What constraints should go in the "Subject to the Constraints" box in the Solver Parameters dialog?
The calculated results in column J should equal the constraints in column H: H4 = J4 and H5 = J5.
Here is the completed worksheet: