Let x1 represent the number of acres of crop A, x2 the number of acres of crop B, and x3 the number of acres of crop C. The acreage constraint is given by:
x1 + x2 + x3 ≤ 100
The limited amount of money available for buying seed leads to this constraint:
x1 acres at 40 dollars/acre is 40x1 dollars x2 acres at 20 dollars/acre is 20x2 dollars x3 acres at 30 dollars/acre is 30x3 dollars 40x1 + 20x2 + 30x3 ≤ 3200
The limited number of workdays leads to this constraint:
x1 acres at 1 workday/acre is x1 workdays x2 acres at 2 workdays/acre is 2x2 workdays x3 acres at 1 workday/acre is x3 workdays x1 + 2x2 + x3 ≤ 160
For the profit, we have:
x1 acres at $100/acre is 100x1 dollars x2 acres at $300/acre is 300x2 dollars x3 acres at $200/acre is 200x3 dollars P = 100x1 + 300x2 + 200x3
Putting it all together, we obtain the following mathematical model.
x1 + x2 + x3 ≤ 100 (available acreage)
40x1 + 20x2 + 30x3 ≤ 3200 (money for seed)
x1 + 2x2 + x3 ≤ 160 {available labor)
P = 100x1 + 300x2 + 200x3 (profit)
x1, x2 ,x3 ≥ 0
Maximize P
Introducing slack variables and rewriting the objective function leads to this mathematical model:
x1 + x2 + x3 + s1 = 100 (available acreage)
40x1 + 20x2 + 30x3 + s2 = 3200 (money for seed)
x1 + 2x2 + x3 + s3 = 160 (available labor)
-100x1 - 300x2 - 200x3 + P = 0 (profit)
x1, x2 ,x3 ,s1, s2, s3 ≥ 0
Maximize P
We can use an augmented matrix to represent the alternate mathematical model. The augmented matrix is indicated by the shaded regions in the table below. The column and row headings help us interpret the matrix. Basic variables correspond to columns in which there is only one nonzero value (typically a value of one). The basic variables have these nonzero values in different rows. The basic variables are listed in the first column of the table.
| Basic Variables | x1 | x2 | x3 | s1 | s2 | s3 | P | |
| s1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 100 |
| s2 | 40 | 20 | 30 | 0 | 1 | 0 | 0 | 3200 |
| s3 | 1 | 2 | 1 | 0 | 0 | 1 | 0 | 160 |
| P | -100 | -300 | -200 | 0 | 0 | 1 | 0 |
This tableaux corresponds to the basic solution: x1 = 0, x2 = 0, x3 = 0, s1 = 100, s2 = 3200, and s3 = 160. For this basic solution, P = 0. A bold font is used to indicate the basic variables.
Identify the column with the most negative value in the bottom row. The variable that corresponds to this pivot column will become a basic variable. It is called an entering variable because it is entering the set of basic variables. In this example, x2 is the entering variable. Within the context of the original problem, planting more of crop B is more profitable than planting an acre of either crop A or crop C so the number of acres of crop B (x2) has the greatest impact when it comes to maximizing the profit.
| Basic Variables | x1 | x2 | x3 | s1 | s2 | s3 | P | |
| s1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 100 |
| s2 | 40 | 20 | 30 | 0 | 1 | 0 | 0 | 3200 |
| s3 | 1 | 2 | 1 | 0 | 0 | 1 | 0 | 160 |
| P | -100 | -300 | -200 | 0 | 0 | 1 | 0 |
Divide each value (except the last) in the right-most column by the corresponding value in the pivot column. If the value in the pivot column is negative or zero, skip that row. Identify the row with the smallest quotient. The variable that corresponds to this pivot row will become a non-basic variable. It is called the exiting variable because it is leaving the set of basic variables. The element at the intersection of the pivot column and the pivot row is the pivot element. The exiting variable in this example is s3 and the pivot element has a value of 2:
| Basic Variables | x1 | x2 | x3 | s1 | s2 | s3 | P | Quotient | |
| s1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 100 | 100 / 1 = 100 |
| s2 | 40 | 20 | 30 | 0 | 1 | 0 | 0 | 3200 | 3200 / 20 = 160 |
| s3 | 1 | 2 | 1 | 0 | 0 | 1 | 0 | 160 | 160 / 2 = 80 |
| P | -100 | -300 | -200 | 0 | 0 | 0 | 1 | 0 |
Perform row operations until the pivot element has a value of 1 and the remaining values in the pivot column are 0.
| Basic Variables | x1 | x2 | x3 | s1 | s2 | s3 | P | Operation | |
| s1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 100 | |
| s2 | 40 | 20 | 30 | 0 | 1 | 0 | 0 | 3200 | |
| s3 | 1 | 2 | 1 | 0 | 0 | 1 | 0 | 160 | R3 = (1/2)*R3 |
| P | -100 | -300 | -200 | 0 | 0 | 0 | 1 | 0 |
*row(1/2, [A], 3)
yields the table below. In this table I am indicating the row operations that need to be performed to get a value of zero in each of the remaining rows of the pivot column. Since these operations are independent of each other, I can list them all at once.
| Basic Variables | x1 | x2 | x3 | s1 | s2 | s3 | P | Operation | |
| s1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 100 | R1 = R1 + (-1)* R3 |
| s2 | 40 | 20 | 30 | 0 | 1 | 0 | 0 | 3200 | R2 = R2 + (-20) * R3 |
| s3 | 1/2 | 1 | 1/2 | 0 | 0 | 1/2 | 0 | 80 | |
| P | -100 | -300 | -200 | 0 | 0 | 0 | 1 | 0 | R4 = R4 + 300 * R3 |
*row+(-1, Ans, 3, 1)*row+(-20, Ans, 3, 2)
*row+(300, Ans, 3, 4)
yields
| Basic Variables | x1 | x2 | x3 | s1 | s2 | s3 | P | |
| s1 | 1/2 | 0 | 1/2 | 1 | 0 | -1/2 | 0 | 20 |
| s2 | 30 | 0 | 20 | 0 | 1 | -10 | 0 | 1600 |
| x2 | 1/2 | 1 | 1/2 | 0 | 0 | 1/2 | 0 | 80 |
| P | 50 | 0 | -50 | 0 | 0 | 150 | 1 | 24000 |
Notice that the third row now corresponds to the entering basic variable x2 rather than the exiting variable s3. Setting the non-basic variables (x1 , x3, and s3) to zero and solving for x2, s1, and s2 yields the basic solution: x1 = 0, x2 = 80, x1 = 0, s1 = 20, s2 = 1600, and s3 = 0 for which P = $24,000.
| Basic Variables | x1 | x2 | x3 | s1 | s2 | s3 | P | |
| s1 | 1/2 | 0 | 1/2 | 1 | 0 | -1/2 | 0 | 20 |
| s2 | 30 | 0 | 20 | 0 | 1 | -10 | 0 | 1600 |
| x2 | 1/2 | 1 | 1/2 | 0 | 0 | 1/2 | 0 | 80 |
| P | 50 | 0 | -50 | 0 | 0 | 150 | 1 | 24000 |
The pivot row is the row corresponding to s1 (the exiting variable) and the value of the pivot element is 1/2.
| Basic Variables | x1 | x2 | x3 | s1 | s2 | s3 | P | Quotient | |
| s1 | 1/2 | 0 | 1/2 | 1 | 0 | -1/2 | 0 | 20 | 20 / (1/2) = 40 |
| s2 | 30 | 0 | 20 | 0 | 1 | -10 | 0 | 1600 | 1600 / 20 = 80 |
| x2 | 1/2 | 1 | 1/2 | 0 | 0 | 1/2 | 0 | 80 | 80 / (1/2) = 160 |
| P | 50 | 0 | -50 | 0 | 0 | 150 | 1 | 24000 |
Perform row operations that result in the pivot element having a value of 1 and all other elements in the pivot column having a value of 0.
| Basic Variables | x1 | x2 | x3 | s1 | s2 | s3 | P | Operation | |
| s1 | 1/2 | 0 | 1/2 | 1 | 0 | -1/2 | 0 | 20 | R1 = 2 * R1 |
| s2 | 30 | 0 | 20 | 0 | 1 | -10 | 0 | 1600 | |
| x2 | 1/2 | 1 | 1/2 | 0 | 0 | 1/2 | 0 | 80 | |
| P | 50 | 0 | -50 | 0 | 0 | 150 | 1 | 24000 |
*row(2, Ans, 1)
yields
| Basic Variables | x1 | x2 | x3 | s1 | s2 | s3 | P | Operation | |
| s1 | 1 | 0 | 1 | 2 | 0 | -1 | 0 | 40 | |
| s2 | 30 | 0 | 20 | 0 | 1 | -10 | 0 | 1600 | R2 = R2 + (-20) * R1 |
| x2 | 1/2 | 1 | 1/2 | 0 | 0 | 1/2 | 0 | 80 | R3 = R3 + (-1/2) * R1 |
| P | 50 | 0 | -50 | 0 | 0 | 150 | 1 | 24000 | R4 = R4 + 50 * R1 |
*row+(-20, Ans, 1, 2)*row+(-.5, Ans, 1, 3)
*row+(50, Ans, 1, 4)
yields
| Basic Variables | x1 | x2 | x3 | s1 | s2 | s3 | P | |
| x3 | 1 | 0 | 1 | 2 | 0 | -1 | 0 | 40 |
| s2 | 10 | 0 | 0 | -40 | 1 | 10 | 0 | 800 |
| x2 | 0 | 1 | 0 | -1 | 0 | 1 | 0 | 60 |
| P | 100 | 0 | 0 | 100 | 0 | 100 | 1 | 26000 |
Notice that in the first row, x3 has become the basic variable replacing s1. Letting the non-basic variables (x1, s1 and s3) equal zero and solving for x2 , x3, and s2 leads to the basic solution: x1 = 0, x2 = 60, x3 = 40, s1 = 0, s2 = 800 and s3 = 0. For this basic solution, P = $26,000.
Since there are no more negative values in the bottom row, the process terminates. We have found the maximum profit of $26,000 which occurs when the farmer plants no crop A, 60 acres of crop B, and 40 acres of crop C. The slack variable s2 is 800 which indicates that the cost of the seed will be $800 less than the farmer could have afforded. That is, the farmer will only pay $2,400 for the seed even though $3,200 was available. The farmer will use all of the acreage and all of the labor that was available.
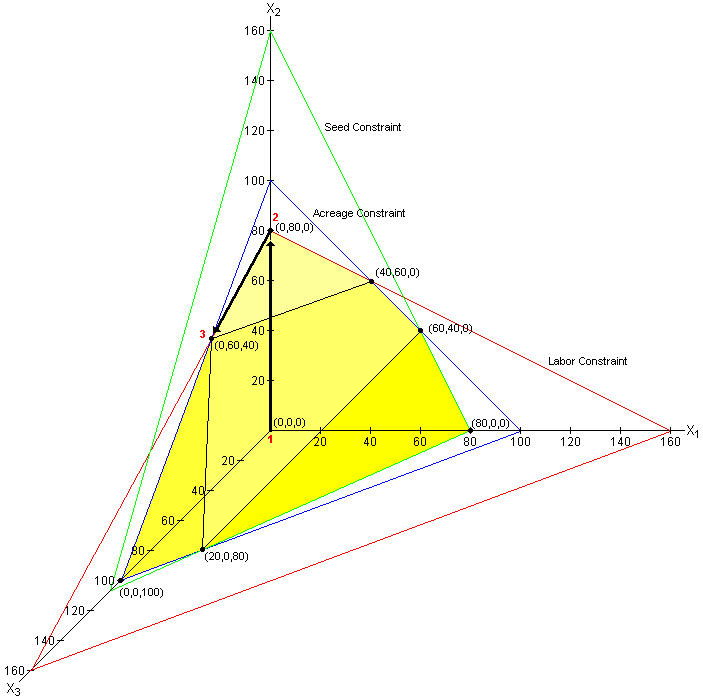
The graph of a function of the form ax1 + bx2 + cx3 = constant is a plane in
three-dimensional space. Consequently, each of the constraints in this problem
is a plane. In the illustration below, the blue lines define the plane
corresponding to the acreage constraint, the green lines define the plane
corresponding to the cost of seed constraint, and the red lines define the plane
that corresponds to the labor constraint.
An inequality in three variables is represented by the space on one side or the other of the corresponding plane. In this example, the origin is on the correct side of all three planes. In the illustration below, the feasible region is a three-dimensional region extending out from the origin (towards the viewer) and bounded by the four shaded faces. The edges of this region are formed by two intersecting planes and each of the eight vertices is at the intersection of three planes. These vertices correspond to the feasible solutions to this system and the maximum profit will occur at one of them. The simplex algorithm visited three of these vertices. The initial simplex tableau corresponds to the origin (zero profit). The second vertex was at (0,80,0) where the profit was $24,000. The final vertex was at (0,60,40) where the maximum profit of $26,000 is achieved.