

Consider this system of linear equations:
Supply: 10p - 4q = 32 Demand: 11p + 19q = 170
In this system, p represents the price of an item in dollars and q represents the quantity in hundreds. The first equation describes the relationship between price and quantity from the perspective of the supplier. The second equation describes the relationship from the perspective of the consumer. Our goal is to solve this system of equations simultaneously.
1. Download and open the file, Lab06.xlsx. Remind me how. Put your name in cell B1 of the supply and demand sheet.
The supply and demand worksheet is set up just a little different than it was on the solver solution worksheet in lab 4. Here is how it was set up in lab 4:
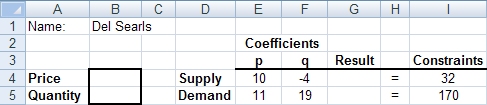
In lab 4 we were using Excel's solver tool to solve the system of equations. That required that we set up constraints involving calculated values (the result in column G) and specific numbers (the constraints in column I). The equal signs in column H remind us that the calculated results are to be equal to the constraint values.
In this lab, however, we are using matrix arithmetic rather than Excel's solver tool so we don't need columns G and H. Our new setup is illustrated here:
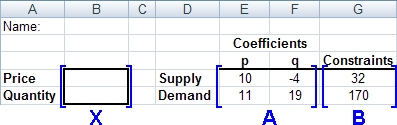
Matrix A is the matrix of coefficients, matrix B is the matrix of constants, and matrix X is the matrix of variables. The problem can be thought of as a matrix equation AX=B which has the solution X=A-1B:
![]()
2. In cells B4:B5 (matrix X) enter the array formula that will
implement A-1B. Don't forget to terminate the entry of the formula
using Ctrl-Shift-Enter. You should get the same values you obtained before
when you used the solver tool to solve this system of equations.
![]()
Parking fees at a municipal zoo are $5.00 for patrons who purchased season passes and $7.50 for all others. On one particular day, a total of 1,200 vehicles used the parking lot and the total receipts were $7,125. How many of these vehicles used season passes and how many did not.
1. Derive a mathematical model (a system of equations) for this problem. It is important that you attempt to do this on your own. If you get stuck, you can click on the following link. Help
2. Activate the parking receipts worksheet and set up your mathematical model. Try to come up with the set up on your own. If you get stuck, you can click on the following link. Help
3. Use an array formula to find the number of vehicles as the solution to a matrix equation: X = A-1B. Try to do this on your own. If you need help, click on the following link. Help
4. You should find that there were 750 cars that used season passes and 450 that did not.
A concert hall has 10,000 seats and two categories of ticket prices, $25 and $35. Assuming that all seats can be sold, how many tickets in each category should be sold to bring in total gate receipts of $275,000?
1. Come up with a mathematical model for this problem. It is important that you attempt to do this on your own. If you get stuck, you can click on the following link. Help
2. On the ticket allocation worksheet, set up your mathematical model.
3. Use an array formula to determine the number of each type of ticket sold. You should find that 7,500 $25 tickets and 2,500 $35 tickets were sold.
A state university system is planning to hire new faculty members at the rank of lecturer or instructor. Each lecturer teaches 6 sections a year and earns an annual salary of $20,000. Each instructor teaches 8 sections a year and earns an annual salary of $25,000. The university needs to cover 66 sections and has a $210,000 budget for the new hires. How many new lecturers and instructors should be hired to exactly meet the demand for sections and to completely exhaust the salary budget?